高等数学之初等变换初等矩阵思维导图

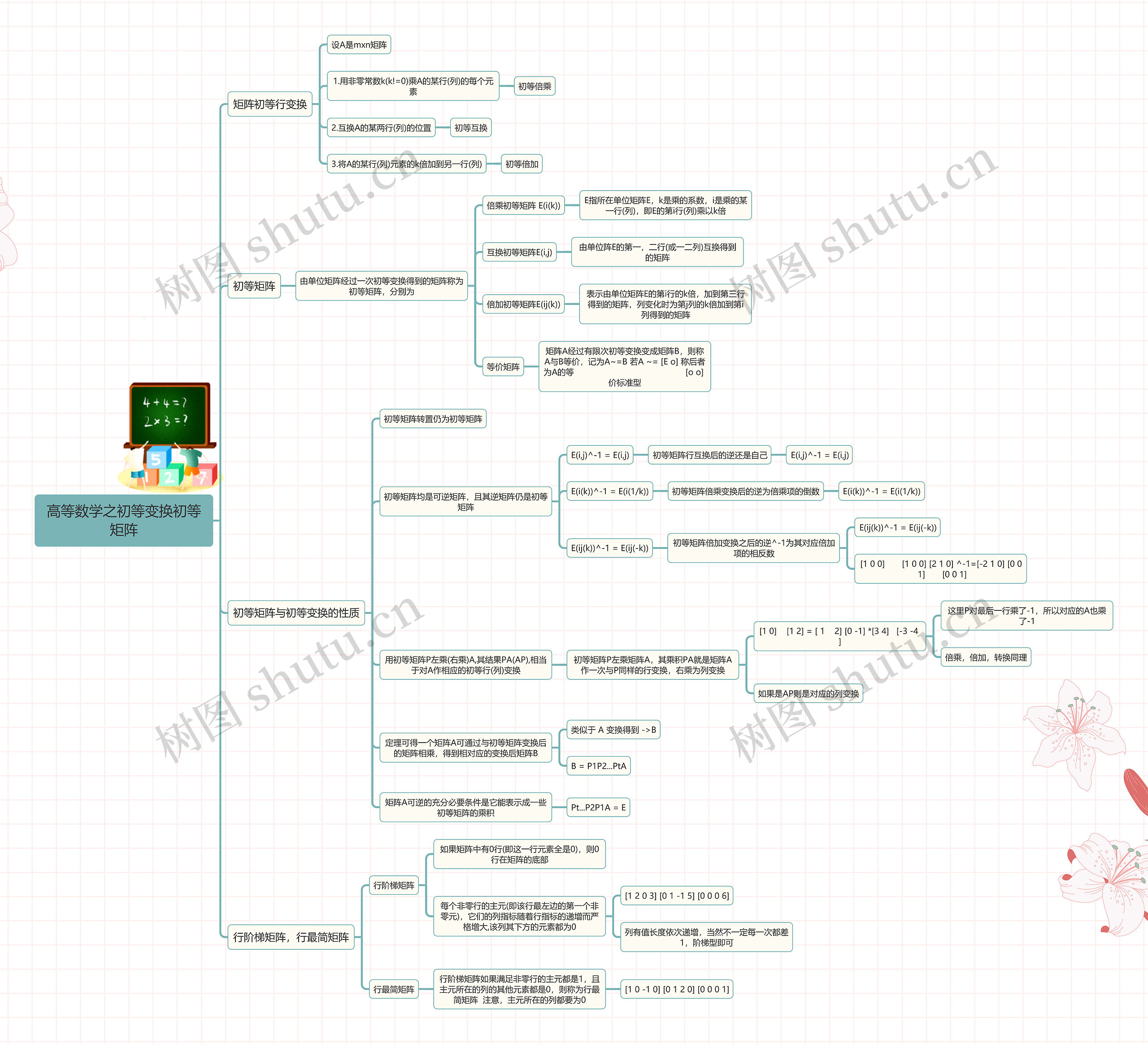
高等数学之初等变换初等矩阵思维导图包含以下知识点：1.矩阵初等行变换，即初等倍乘、初等互换、初等倍加。

2.初等矩阵/的定义和分类，包含倍乘初等矩阵、互换初等矩阵、倍加初等矩阵。

3.等价矩阵/的概念，和矩阵的等价标准型。

4.初等矩阵/与初等变换的性质，如初等矩阵的转置、可逆性、行互换后的逆还是自己、倍乘变换后的逆为倒数、倍加变换后的逆为相反数等。

5.用初等矩阵进行矩阵的变换，包含左乘和右乘，能得到对应的矩阵初等行列变换。

6.定理：一个矩阵可通过与初等矩阵变换后的矩阵相乘，得到相对应的变换后矩阵，矩阵A可逆的充分必要条件是他能表示成一些初等矩阵的乘积。

7.行阶梯矩阵/和行最简矩阵，行最简矩阵是行阶梯矩阵的一种特殊形式，即每个非零行的主元都是1，且主元所在的列的其他元素都是0。

初等变换和初等矩阵思维导图的知识点包含初等变换的三种类型，如初等倍乘、初等互换、初等倍加。初等矩阵由单位矩阵经过一次初等变换得到，共有三类，分别是倍乘初等矩阵、互换初等矩阵、倍加初等矩阵，对于矩阵的可逆性和等价矩阵的概念，初等矩阵与初等变换的性质，可以用初等矩阵进行矩阵的变换，得到对应的矩阵初等行列变换。定理告诉我们：一个矩阵可通过与初等矩阵变换后的矩阵相乘，得到相对应的变换后矩阵，矩阵A可逆的充分必要条件是他能表示成一些初等矩阵的乘积，最后介绍了行阶梯矩阵和行最简矩阵，行最简矩阵是行阶梯矩阵的一种特殊形式。