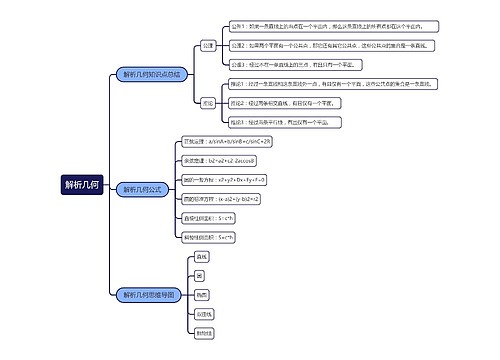
高中数学解析几何中求参数取值范围的方法思维导图

失落感

2023-04-20

浏览量: 10

高中数学

解析几何参数取值范围

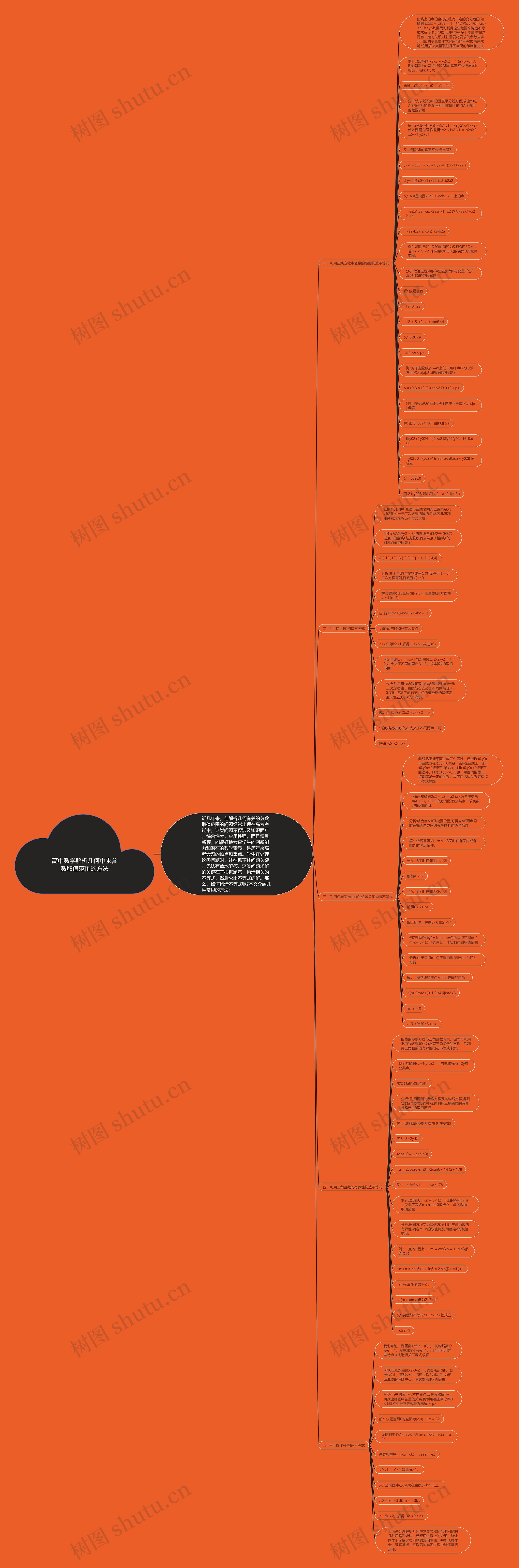
近几年来，与解析几何有关的参数取值范围的问题经常出现在高考考试中，这类问题不仅涉及知识面广，综合性大，应用性强，而且情景新颖，

树图思维导图提供《高中数学解析几何中求参数取值范围的方法》在线思维导图免费制作，点击“编辑”按钮，可对《高中数学解析几何中求参数取值范围的方法》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：0ea8acb8f29b8613a797f3924761f109

思维导图大纲

近几年来，与解析几何有关的参数取值范围的问题经常出现在高考考试中，这类问题不仅涉及知识面广，综合性大，应用性强，而且情景新颖，能很好地考查学生的创新能力和潜在的数学素质，是历年来高考命题的热点和重点。学生在处理这类问题时，往往抓不住问题关键，无法有效地解答，这类问题求解的关键在于根据题意，构造相关的不等式，然后求出不等式的解。那么，如何构造不等式呢?本文介绍几种常见的方法：

一、利用曲线方程中变量的范围构造不等式

曲线上的点的坐标往往有一定的变化范围,如椭圆 x2a2 + y2b2 = 1上的点P(x,y)满足-a≤x≤a,-b≤y≤b,因而可利用这些范围来构造不等式求解,另外,也常出现题中有多个变量,变量之间有一定的关系,往往需要将要求的参数去表示已知的变量或建立起适当的不等式,再来求解.这是解决变量取值范围常见的策略和方法.

例1 已知椭圆 x2a2 + y2b2 = 1 (a>b>0), A,B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0 , 0)

求证:-a2-b2a ≤ x0 ≤ a2-b2a

分析:先求线段AB的垂直平分线方程,求出x0与A,B横坐标的关系,再利用椭圆上的点A,B满足的范围求解.

解: 设A,B坐标分别为(x1,y1) ,(x2,y2),(x1≠x2)代入椭圆方程,作差得: y2-y1x2-x1 =-b2a2 ?x2+x1 y2+y1

又∵线段AB的垂直平分线方程为

y- y1+y22 =- x2-x1 y2-y1 (x-x1+x22 )

令y=0得 x0=x1+x22 ?a2-b2a2

又∵A,B是椭圆x2a2 + y2b2 = 1 上的点

∴-a≤x1≤a, -a≤x2≤a, x1≠x2 以及-a≤x1+x22 ≤a

∴ -a2-b2a ≤ x0 ≤ a2-b2a

例2 如图,已知△OFQ的面积为S,且OF?FQ=1,若 12 < S <2 ,求向量OF与FQ的夹角θ的取值范围.

分析:须通过题中条件建立夹角θ与变量S的关系,利用S的范围解题.

解: 依题意有

∴tanθ=2S

∵12 < S <2 ∴1< tanθ<4

又∵0≤θ≤π

∴π4 <θ

例3对于抛物线y2=4x上任一点Q,点P(a,0)都满足|PQ|≥|a|,则a的取值范围是 ( )

A a<0 B a≤2 C 0≤a≤2 D 0<2

分析:直接设Q点坐标,利用题中不等式|PQ|≥|a| 求解.

解: 设Q( y024 ,y0) 由|PQ| ≥a

得y02+( y024 -a)2≥a2 即y02(y02+16-8a) ≥0

∵y02≥0 ∴(y02+16-8a) ≥0即a≤2+ y028 恒成立

又∵ y02≥0

而 2+ y028 最小值为2 ∴a≤2 选( B )

二、利用判别式构造不等式

在解析几何中,直线与曲线之间的位置关系,可以转化为一元二次方程的解的问题,因此可利用判别式来构造不等式求解.

例4设抛物线y2 = 8x的准线与x轴交于点Q,若过点Q的直线L与抛物线有公共点,则直线L的斜率取值范围是 ( )

A [-12 ,12 ] B [-2,2] C [-1,1] D [-4,4]

分析:由于直线l与抛物线有公共点,等价于一元二次方程有解,则判别式△≥0

解:依题意知Q坐标为(-2,0) , 则直线L的方程为y = k(x+2)

由得 k2x2+(4k2-8)x+4k2 = 0

∵直线L与抛物线有公共点

∴△≥0 即k2≤1 解得-1≤k≤1 故选 (C)

例5 直线L: y = kx+1与双曲线C: 2x2-y2 = 1的右支交于不同的两点A、B，求实数k的取值范围.

分析:利用直线方程和双曲线方程得到x的一元二次方程,由于直线与右支交于不同两点,则△>0,同时,还需考虑右支上点的横坐标的取值范围来建立关于k的不等式.

解：由得 (k2-2)x2 +2kx+2 = 0

∵直线与双曲线的右支交于不同两点，则

解得 -2<-2

三、利用点与圆锥曲线的位置关系构造不等式

曲线把坐标平面分成三个区域，若点P(x0,y0)与曲线方程f(x,y)=0关系：若P在曲线上，则f(x0,y0)=0;若P在曲线内，则f(x0,y0)<0;若P在曲线外，则f(x0,y0)>0;可见，平面内曲线与点均满足一定的关系。故可用这些关系来构造不等式解题.

例6已知椭圆2x2 + y2 = a2 (a>0)与连结两点A(1,2)、B(2,3)的线段没有公共点，求实数a的取值范围.

分析:结合点A,B及椭圆位置,可得当AB两点同时在椭圆内或同时在椭圆外时符合条件.

解：依题意可知，当A、B同时在椭圆内或椭圆外时满足条件。

当A、B同时在椭圆内，则

解得a >17

当A、B同时在椭圆外，则

解得0<6

综上所述，解得0<6 或a>17

例7若抛物线y2=4mx (m≠0)的焦点在圆(x-2m)2+(y-1)2=4的内部，求实数m的取值范围.

分析:由于焦点(m,0)在圆内部,则把(m,0)代入可得.

解：∵抛物线的焦点F(m,0)在圆的内部，

∴(m-2m)2+(0-1)2<4 即m2<3

又∵m≠0

∴-3 <0或0<3

四、利用三角函数的有界性构造不等式

曲线的参数方程与三角函数有关，因而可利用把曲线方程转化为含有三角函数的方程，后利用三角函数的有界性构造不等式求解。

例8 若椭圆x2+4(y-a)2 = 4与抛物线x2=2y有公共点,

求实数a的取值范围.

分析: 利用椭圆的参数方程及抛物线方程,得到实数a与参数θ的关系,再利用三角函数的有界性确定a的取值情况.

解：设椭圆的参数方程为 (θ为参数)

代入x2=2y 得

4cos2θ= 2(a+sinθ)

∴a = 2cos2θ-sinθ=-2(sinθ+ 14 )2+ 178

又∵-1≤sinθ≤1，∴-1≤a≤178

例9 已知圆C：x2 +(y-1)2= 1上的点P(m,n)，使得不等式m+n+c≥0恒成立，求实数c的取值范围

分析:把圆方程变为参数方程,利用三角函数的有界性,确定m+n的取值情况,再确定c的取值范围.

解：∵点P在圆上，∴m = cosβ,n = 1+sinβ(β为参数)

∵m+n = cosβ+1+sinβ = 2 sin(β+ π4 )+1

∴m+n最小值为1-2 ，

∴-(m+n)最大值为2 -1

又∵要使得不等式c≥-(m+n) 恒成立

∴c≥2 -1

五、利用离心率构造不等式

我们知道，椭圆离心率e∈(0,1)，抛物线离心率e = 1，双曲线离心率e>1，因而可利用这些特点来构造相关不等式求解.

例10已知双曲线x2-3y2 = 3的右焦点为F，右准线为L，直线y=kx+3通过以F为焦点,L为相应准线的椭圆中心，求实数k的取值范围.

分析:由于椭圆中心不在原点,故先设椭圆中心,再找出椭圆中各量的关系,再利用椭圆离心率0<1,建立相关不等式关系求解.

解：依题意得F的坐标为(2,0)，L:x = 32

设椭圆中心为(m,0)，则 m-2 =c和 m-32 = a2c

两式相除得: m-2m-32 = c2a2 = e2

∵0<1，∴0<1,解得m>2，

又∵当椭圆中心(m,0)在直线y=kx+3上，

∴0 = km+3 ,即m = - 3k ,

∴- 3k >2，解得-32 <0

上面是处理解析几何中求参数取值范围问题的几种思路和求法，希望通过以上的介绍，能让同学们了解这类问题的常用求法，并能认真体会、理解掌握，在以后的学习过程中能够灵活运用。

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图

U633687664

3.9

树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc

二手书销售平台新航标思维导图

U482683014

1.9

树图思维导图提供《二手书销售平台新航标》在线思维导图免费制作，点击“编辑”按钮，可对《二手书销售平台新航标》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：a92403b70afada50cf4fa4f56e0981c9

思维导图模板

基础教育

数学

正文

相似思维导图模版

4.1.1椭圆的标准方程思维导图

2024-05-29 14:30:14

高二数学复习方法：数学重在培养分析判断思维导图

2023-04-20 17:10:59

极限极限求解方法及举例和极限在实际生活中的运用思维导图

思维导图模版推荐

高二物理复习方法：能量守恒定律公式思维导图

2023-04-20 17:17:29

语文必备：现代哲理诗句精选汇总思维导图

2023-04-20 17:17:29

首页

我的文件

我的团队

个人中心

高中数学解析几何中求参数取值范围的方法思维导图

思维导图大纲

相关思维导图模版

相似思维导图模版

思维导图模版推荐