高一数学集合教案思维导图
拾人心
2023-04-04

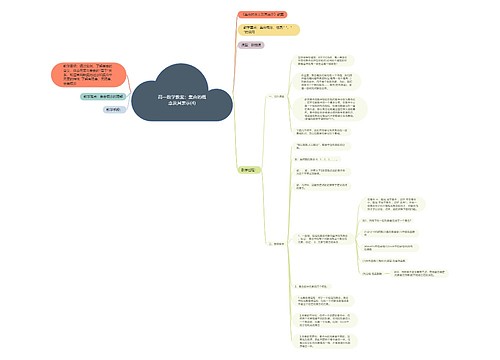
作为一名老师,写好教案是提高教学效率的关键,本模板介绍了高一数学集合教案的知识点,包含教学目的、重点、难点、授课类型、课时安排、教具和教学内容,学习此课可以初步理解集合的概念、思考“属于”关系的意义、认识有限集、无限集、空集的取值范围等内容,教学过程包含复习引入、讲解新课、练习题和小结,通过整体把握、抓大放小的方法,能更好的应对高中数学考试。
思维导图大纲
相关思维导图模版
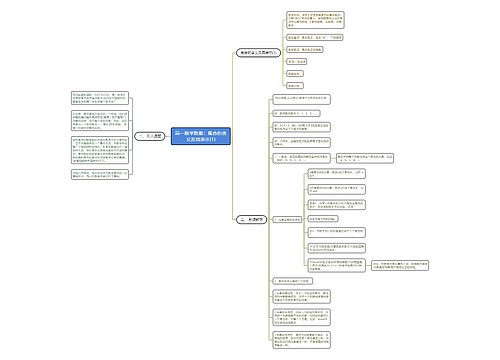
高一数学集合教案范文思维导图
 定格苍凉
定格苍凉树图思维导图提供《高一数学集合教案范文》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学集合教案范文》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:779b8f9521507c66516a07a47f4045dc
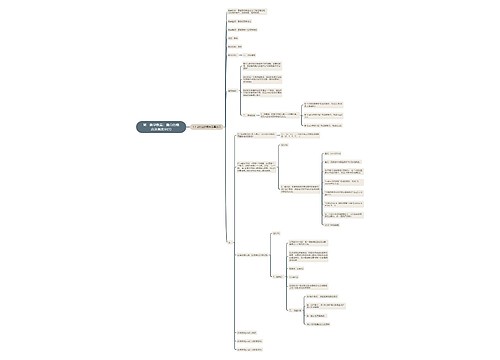
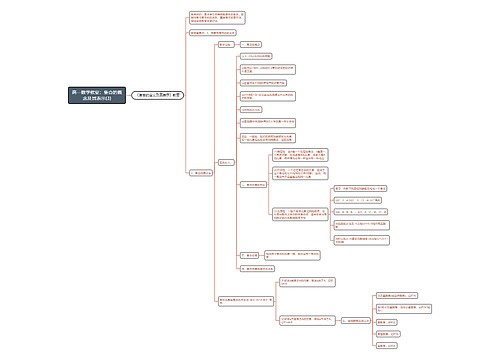
高一数学教案:集合的概念及其表示(4)思维导图
 当居者的迷
当居者的迷树图思维导图提供《高一数学教案:集合的概念及其表示(4)》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:集合的概念及其表示(4)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:eaa845a31d4a1db4195542679ea84d21