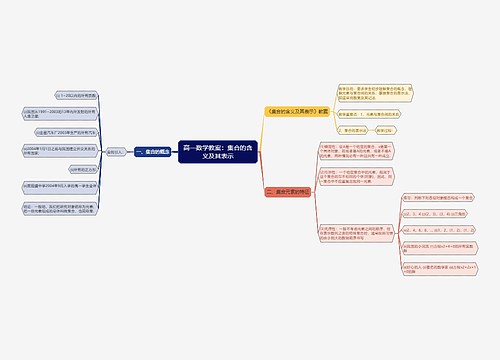
高一数学教案:集合的概念及其表示(4)思维导图
当居者的迷
2023-04-20
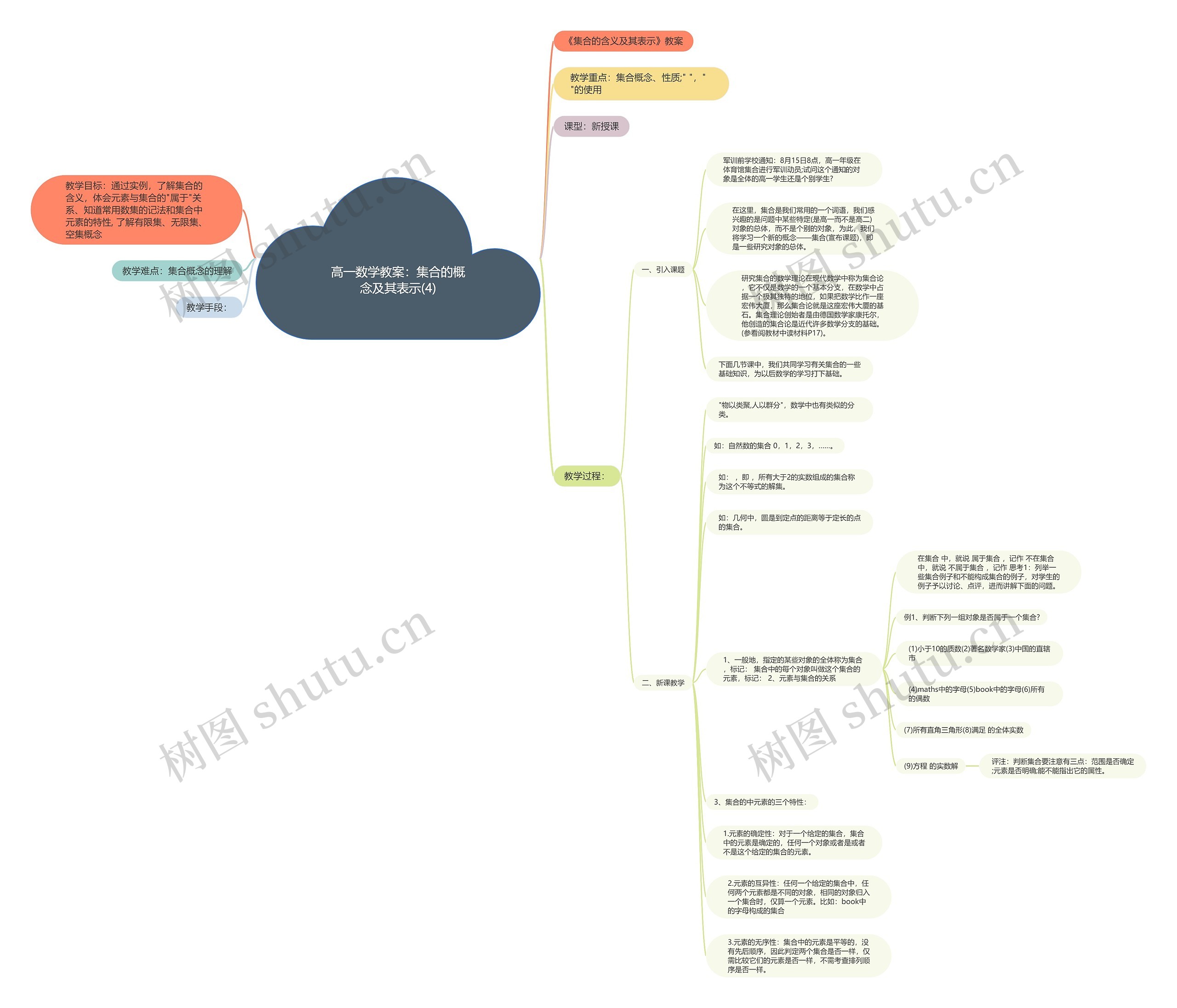
教案通常又叫教学设计,包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等。树图网为大家整理了《高一数学教案:集合的概念及其表示(4)》,供大家参考。
树图思维导图提供《高一数学教案:集合的概念及其表示(4)》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:集合的概念及其表示(4)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:eaa845a31d4a1db4195542679ea84d21
思维导图大纲
相关思维导图模版
高一数学教案:集合的概念及其表示(3)思维导图
 谎话最甜
谎话最甜树图思维导图提供《高一数学教案:集合的概念及其表示(3)》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:集合的概念及其表示(3)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f1242ec52f2193f513261d964b4f9f91
高一数学教案:集合的含义及其表示思维导图
 补偿
补偿树图思维导图提供《高一数学教案:集合的含义及其表示》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教案:集合的含义及其表示》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c4ab322d0d7775e34babdd5530b4bcdc