树图网

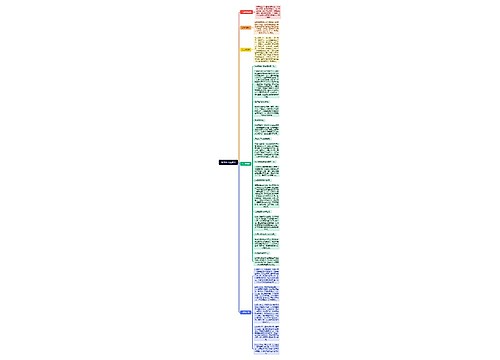
现代控制理论Modern Control Theory思维导图

U9106782758
2025-08-26
浏览量: 0
现代控制理论Modern Control Theory
控制理论
能控性
能观性

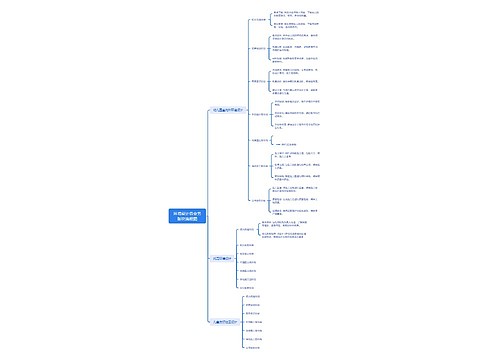
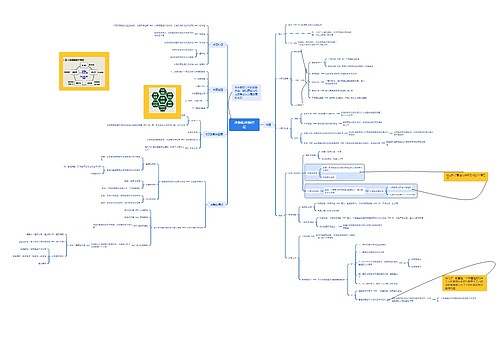
概念，能控性与能观性相关内容讲解

树图思维导图提供《现代控制理论Modern Control Theory》在线思维导图免费制作，点击“编辑”按钮，可对《现代控制理论Modern Control Theory》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：57467a9994b59ef9894605c145356ada

思维导图大纲

相关思维导图模版

（一）诸子百家学说——儒学产生的土壤（23分钟）思维导图
U982226919
2.42
树图思维导图提供《（一）诸子百家学说——儒学产生的土壤（23分钟）》在线思维导图免费制作，点击“编辑”按钮，可对《（一）诸子百家学说——儒学产生的土壤（23分钟）》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：61d7b901b01e24c661b919301dc1d26a
（一）诸子百家学说——儒学产生的土壤（23分钟）
辅导员队伍建设思维导图
:)
4.8
树图思维导图提供《辅导员队伍建设》在线思维导图免费制作，点击“编辑”按钮，可对《辅导员队伍建设》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：660abcadc2f7924e5c9f9690c9447d4c
辅导员队伍建设
思维导图模板行业/职业模板其他正文

相似思维导图模版

主机安全防御思维导图
2024-11-13 11:28:28
主机安全防御
人机料环鱼骨图思维导图
2024-07-29 16:27:50
人机料环鱼骨图
项目二 旅游简史思维脑图思维导图
2024-01-22 19:09:23
项目二 旅游简史思维脑图
电工电子基础脑图思维导图
2023-12-04 02:00:36
电工电子基础脑图
环境设计各业务版块流程图思维导图
2024-11-13 10:05:12
环境设计各业务版块流程图
决策和决策过程思维导图
2024-03-24 21:17:27
决策和决策过程

思维导图模版推荐

总指挥董世伟思维导图
2025-08-27 03:15:19
总指挥董世伟
电机与拖动 Electrical Machine and Dragging思维导图
2025-08-27 12:57:43
电机与拖动 Electrical Machine and Dragging
嵌入式操作系统Embedded Operating System思维导图
2025-08-27 13:01:02
嵌入式操作系统Embedded Operating System
九年级上册重点思维导图
2025-08-26 17:04:26
九年级上册重点
物理四单元重点思维导图
2025-08-26 15:54:37
物理四单元重点
未来教师“素养—角色—能力”图谱思维导图
2025-08-26 00:56:07
未来教师“素养—角色—能力”图谱
首页
我的文件
我的团队
个人中心