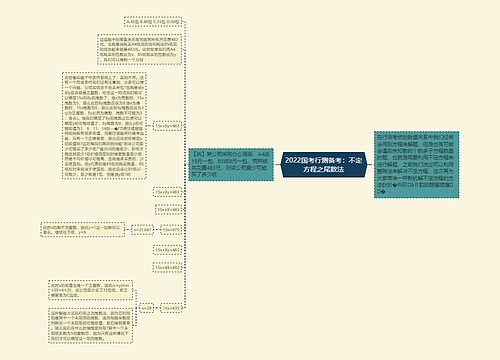
2022国考行测数量关系在演绎推理中的妙用思维导图
风雪夜人归
2023-03-04
华图教育为大家整理了行测备考相关知识供广大考生复习，更多备考技巧请持续关注华图教育。
树图思维导图提供《2022国考行测数量关系在演绎推理中的妙用》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测数量关系在演绎推理中的妙用》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：cbe30f4fb0d4063dfe2a8cbceb0bb004
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
埃隆·马斯克的商业版图思维导图
乐农树图思维导图提供《埃隆·马斯克的商业版图》在线思维导图免费制作，点击“编辑”按钮，可对《埃隆·马斯克的商业版图》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：7464362ac911e8a334867bb3fc7a2346
