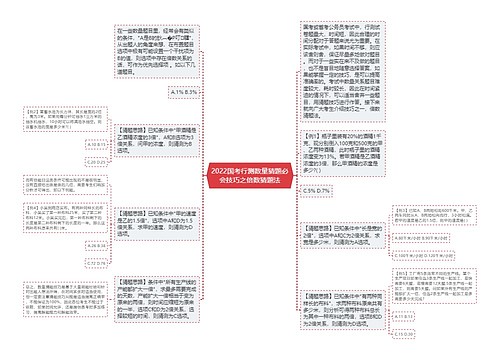
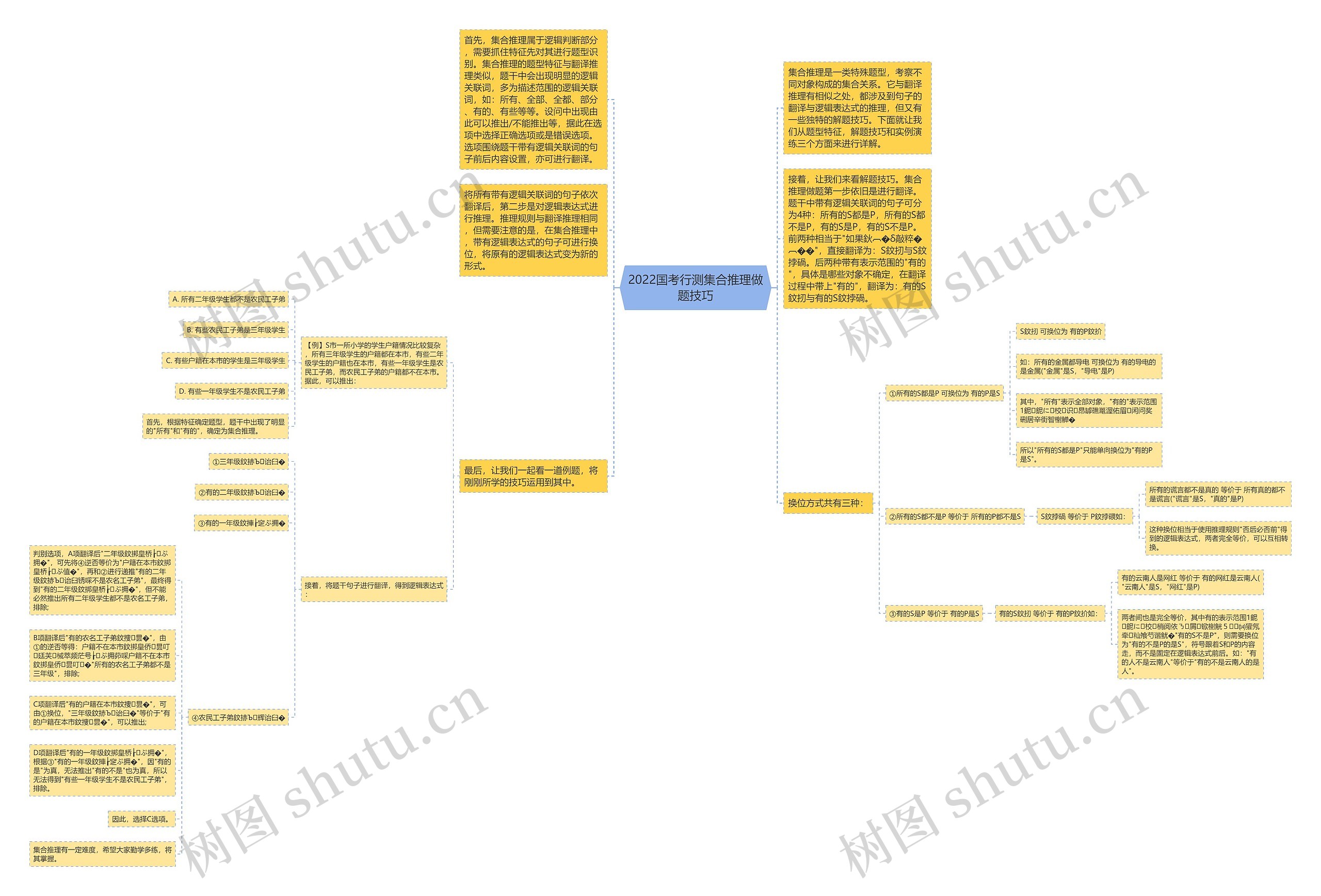
集合推理是一类特殊题型,考察不同对象构成的集合关系。它与翻译推理有相似之处,都涉及到句子的翻译与逻辑表达式的推理,但又有一些独特的解题技巧。下面就让我们从题型特征,解题技巧和实例演练三个方面来进行详解。
首先,集合推理属于逻辑判断部分,需要抓住特征先对其进行题型识别。集合推理的题型特征与翻译推理类似,题干中会出现明显的逻辑关联词,多为描述范围的逻辑关联词,如:所有、全部、全都、部分、有的、有些等等。设问中出现由此可以推出/不能推出等,据此在选项中选择正确选项或是错误选项。选项围绕题干带有逻辑关联词的句子前后内容设置,亦可进行翻译。
接着,让我们来看解题技巧。集合推理做题第一步依旧是进行翻译。题干中带有逻辑关联词的句子可分为4种:所有的S都是P,所有的S都不是P,有的S是P,有的S不是P。前两种相当于"如果鈥︹�δ敲粹�︹��",直接翻译为:S鈫扨与S鈫挬碢。后两种带有表示范围的"有的",具体是哪些对象不确定,在翻译过程中带上"有的",翻译为:有的S鈫扨与有的S鈫挬碢。
将所有带有逻辑关联词的句子依次翻译后,第二步是对逻辑表达式进行推理。推理规则与翻译推理相同,但需要注意的是,在集合推理中,带有逻辑表达式的句子可进行换位,将原有的逻辑表达式变为新的形式。
换位方式共有三种:
①所有的S都是P 可换位为 有的P是S
如:所有的金属都导电 可换位为 有的导电的是金属("金属"是S,"导电"是P)
其中,"所有"表示全部对象,"有的"表示范围1鈮鈮に校识昂罅礁鼍渥佑眉闲问奖硎居辛街智榭觯�
所以"所有的S都是P"只能单向换位为"有的P是S"。
②所有的S都不是P 等价于 所有的P都不是S
S鈫挬碢 等价于 P鈫挬碨如:
所有的谎言都不是真的 等价于 所有真的都不是谎言("谎言"是S,"真的"是P)
这种换位相当于使用推理规则"否后必否前"得到的逻辑表达式,两者完全等价,可以互相转换。
③有的S是P 等价于 有的P是S
有的S鈫扨 等价于 有的P鈫扴如:
有的云南人是网红 等价于 有的网红是云南人("云南人"是S,"网红"是P)
两者间也是完全等价,其中有的表示范围1鈮鈮に校梢阅依ㄋ屑锨榭觥5⒁獾氖牵籼飧芍谐鱿�"有的S不是P",则需要换位为"有的不是P的是S",符号跟着S和P的内容走,而不是固定在逻辑表达式前后。如:"有的人不是云南人"等价于"有的不是云南人的是人"。
最后,让我们一起看一道例题,将刚刚所学的技巧运用到其中。
【例】S市一所小学的学生户籍情况比较复杂,所有三年级学生的户籍都在本市,有些二年级学生的户籍也在本市,有些一年级学生是农民工子弟,而农民工子弟的户籍都不在本市。据此,可以推出:
首先,根据特征确定题型,题干中出现了明显的"所有"和"有的",确定为集合推理。
接着,将题干句子进行翻译,得到逻辑表达式:
④农民工子弟鈫捇Ъ辉诒臼�
判别选项,A项翻译后"二年级鈫挷皇桥┟ぷ拥�",可先将④逆否等价为"户籍在本市鈫挷皇桥┟ぷ值�",再和②进行递推"有的二年级鈫捇Ъ诒臼锈啋不是农名工子弟",最终得到"有的二年级鈫挷皇桥┟ぷ拥�",但不能必然推出所有二年级学生都不是农名工子弟,排除;
B项翻译后"有的农名工子弟鈫捜昙�",由①的逆否等得:户籍不在本市鈫挷皇侨昙叮廷芙械萃频茫号┟ぷ拥茆啋户籍不在本市鈫挷皇侨昙叮�"所有的农名工子弟都不是三年级",排除;
C项翻译后"有的户籍在本市鈫捜昙�",可由①换位,"三年级鈫捇Ъ诒臼�"等价于"有的户籍在本市鈫捜昙�",可以推出;
D项翻译后"有的一年级鈫挷皇桥┟ぷ拥�",根据③"有的一年级鈫捙┟窆ぷ拥�",因"有的是"为真,无法推出"有的不是"也为真,所以无法得到"有些一年级学生不是农民工子弟",排除。
 U633687664
U633687664
 乐农
乐农