树图网

2022国考行测备考干货之几何尺度扩大原理思维导图

旧街悲巷
2023-03-04
浏览量: 0
2022国考行测备考干货之几何尺度扩大原理
2022国考
行测
几何尺度扩大原理

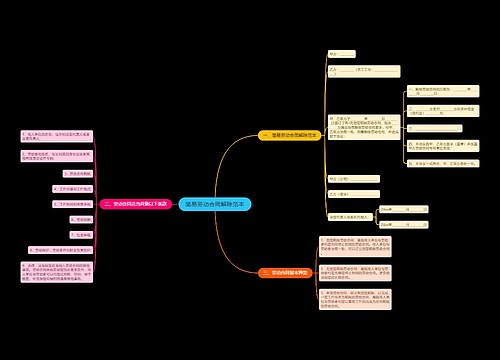
几何问题无论在国考、省考还是事业考试当中此类问题都属于高频考点，在几何问题当中主要考察大家几何计算和几何性质。在这里主要为大家介绍关于几何尺度扩大理论如何应用以及相对应易错点和难点。

树图思维导图提供《2022国考行测备考干货之几何尺度扩大原理》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测备考干货之几何尺度扩大原理》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：6b52fbeaeb8c037343f71203e0905f5b

思维导图大纲

相关思维导图模版

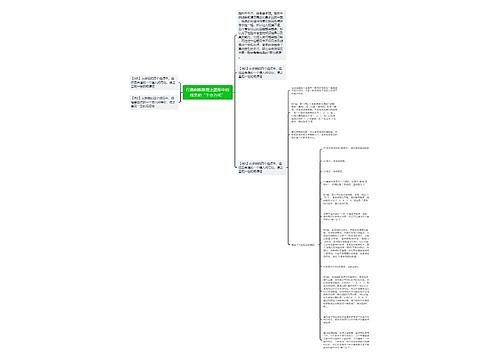
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664
3.9
树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查
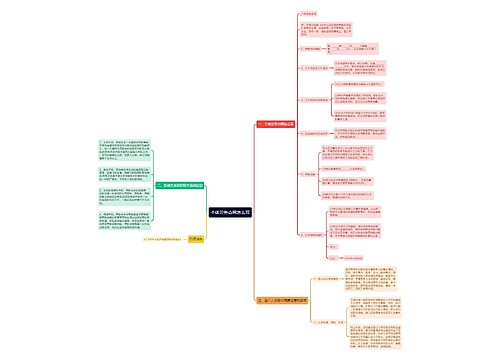
埃隆·马斯克的商业版图思维导图
乐农
0.68
树图思维导图提供《埃隆·马斯克的商业版图》在线思维导图免费制作，点击“编辑”按钮，可对《埃隆·马斯克的商业版图》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：7464362ac911e8a334867bb3fc7a2346
埃隆·马斯克的商业版图
思维导图模板资格考试公务员考试正文

相似思维导图模版

行测知识点（三）思维导图
2022-08-15 19:34:02
行测知识点（三）
行测知识点（十四）思维导图
2022-08-16 10:17:45
行测知识点（十四）
行测常识：中国近代史时间轴思维导图
2022-07-26 20:47:24
行测常识：中国近代史时间轴
公考基30个必知汇总树形图思维导图
2022-07-20 18:45:19
公考基30个必知汇总树形图
国考行测——资料分析考点思维导图
2022-07-03 17:46:50
国考行测——资料分析考点
公考政治常识马哲思维导图
2022-07-27 13:03:33
公考政治常识马哲思维导图

思维导图模版推荐

简易劳动合同解除范本思维导图
2023-03-04 02:25:17
简易劳动合同解除范本
孕妇劳动合同解除的赔偿标准思维导图
2023-03-04 02:25:13
孕妇劳动合同解除的赔偿标准
公务员行测备考技巧之图形推理中“功能线条”的妙用思维导图
2023-03-04 02:25:10
公务员行测备考技巧之图形推理中“功能线条”的妙用
2022国考行测备考干货之奇偶特性思维导图
2023-03-04 02:25:06
2022国考行测备考干货之奇偶特性
行测判断推理之图形中的线条的“千变万化”思维导图
2023-03-04 02:25:19
行测判断推理之图形中的线条的“千变万化”
个体劳务合同怎么写思维导图
2023-03-04 02:25:22
个体劳务合同怎么写
首页
我的文件
我的团队
个人中心