2022国考行测行程问题-环形相遇追及思维导图
没顾忌
2023-03-04
在我们备考公考的过程中，行程问题可谓是一个热门考点，有些题目看起来晦涩难懂，但是如果学会了一些方法之后，再看这些题目，反而觉得并没有那么难了。那么，今天呢，咱们就先看一看行程里的环形相遇追及问题。
树图思维导图提供《2022国考行测行程问题-环形相遇追及》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测行程问题-环形相遇追及》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：fa715fba7e161302879cc9d1dea07d27
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
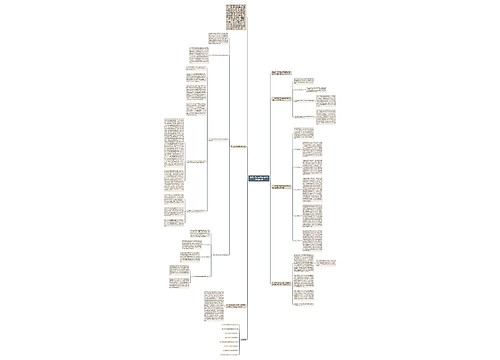
广播电视奖项及评奖标准思维导图
U782682106树图思维导图提供《广播电视奖项及评奖标准》在线思维导图免费制作，点击“编辑”按钮，可对《广播电视奖项及评奖标准》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：a4210651fa3a78355ac9f5101bb2c616
