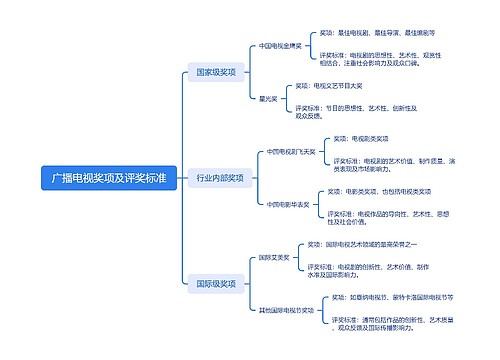
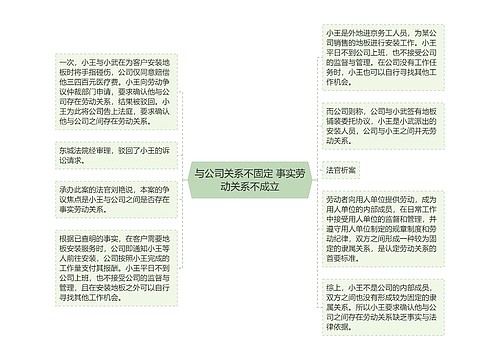
在国考行测考试中数量关系一直是广大考生最头疼的模块，数量关系模块题型较多计算量也较大，今天就让我们了解一下数量关系模块中出现频率较高也比较好拿分的题型-工程问题。那这类题型又是以哪种方式出现，解题中又有哪些技巧呢?今天让我们一起来学习一下。
方法：一般通过赋值工作总量为工作时间的公倍数(或最小公倍数)进行赋值计算
【例1】手工制作一批元宵节花灯，甲、乙丙三位师傅单独做，分别需要40小时、48小时、60小时完成。如果三位师傅共同制作4小时后，剩余任务由乙、丙一起完成，则乙在整个花灯制作过程中所投入的时间是：( )
【答案】A【解析】赋值总量为240，则甲乙丙的效率分别为6、5、4，设乙用时t，根据题意得：(6+5+4)脳4+(5+4)脳(t-4)=240，解得t=24。因此，本题选项为A。
【例2】一项工程，甲、乙合作16天完成，乙、丙合作12天完成，丙、丁合作16天完成，如果甲、丁合作完成这项工程需要多少天?( )
【答案】B【解析】令工作总量为48，则甲乙丙丁的工作效率满足：甲+乙=3，乙+丙=4，丙+丁=3，进而可求得：甲+丁=2，所以需要48梅2=24天。因此，本题选项为B。
特征：题目中不仅给定工作时间，还给出与效率相关的某个逻辑关系
方法：一般优先寻找效率之间的比例关系进行赋值，再求工作总量，最终求出相应结果
【例3】甲、乙、丙三人共同完成一项工程，他们的工作效率之比是5∶4∶6。先由甲、乙两人合做6天，再由乙单独做9天，完成全部工程的60%。若剩下的工程由丙单独完成，则丙所需要的天数是?( )
【答案】C【解析】设甲、乙、丙三人的效率为5、4、6，则已完成6脳(5+4)+4脳9=90，占60%，则剩下的40%的工作量为90梅0.6脳0.4=60，丙需60梅6=10(天)完成。因此，本题选项为C。
【例4】甲、乙、丙三个工程队的效率比为6∶5∶4，现将A、B两项工作量相同的工程交给这三个工程队，甲队负责A工程，乙队负责B工程，丙队参与A工程若干天后转而参与B工程，两项工程同时开工，耗时16天同时结束。问丙队在A工程中参与施工多少天?( )
【答案】A【解析】赋值甲、乙、丙工作效率分别为6、5、4，设丙在A工程中做了x天，则A工程工作量为：6脳16+4x，B工程工作量为5脳16+4脳(16-x)，两项工程工作量相同，解得x=6。因此，本题选项为A。
特征：不仅给工作时间还给工作效率、工作量的前后变化
方法：找出工作量、效率、时间等的前后变化的关系，整体考虑进行列式
【例5】工程队接到一项工程，投入80台挖掘机。如连续施工30天，每天工作10小时，正好按期完成。但施工过程中遭遇大暴雨，有10天时间无法施工。工期还剩8天时，工程队增派70台挖掘机并加班施工。若工程队想按期完成，则平均每天需多工作多少个小时( )。
【答案】B【解析】工期一共需要80脳30脳10=24000(小时)。由题意知增派挖掘机之前一共工作了30-10-8=12(天)，完成了80脳12脳10=9600(小时)，还需要24000-9600=14400(小时)。剩下的工程量需要8天完成，则每天需要工作14400梅8梅(80+70)=12(小时)，每天需要多工作12-10=2(小时)。因此，本题选项为B。
以上就是我们工程问题中常见的三种题型-给定时间型、效率制约型以及条件综合型，大家要掌握这类题型的特征及解题方法，并且不断的进行刷题练习，提高做题速度，这类题
U769027638
U464287897
