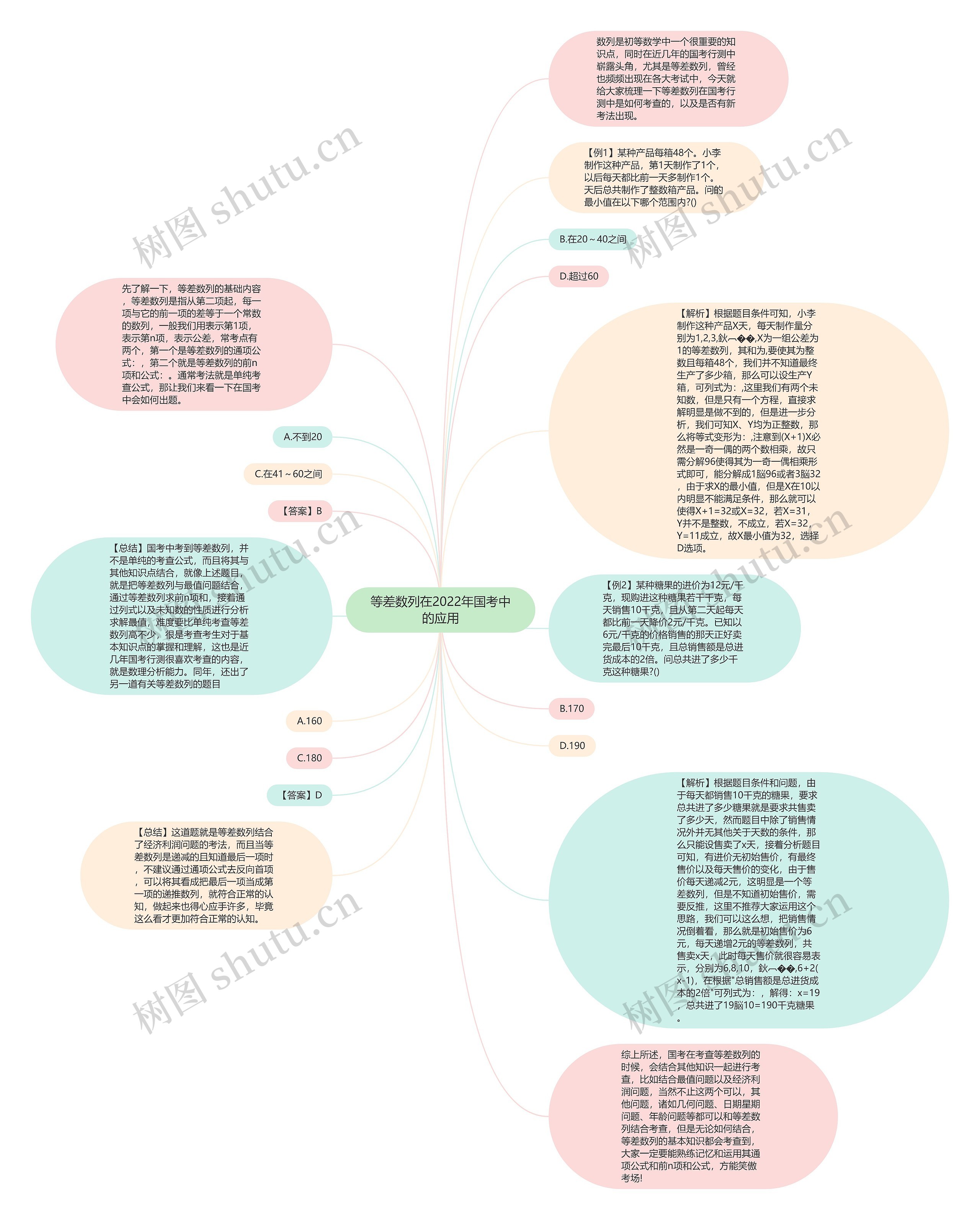
数列是初等数学中一个很重要的知识点,同时在近几年的国考行测中崭露头角,尤其是等差数列,曾经也频频出现在各大考试中,今天就给大家梳理一下等差数列在国考行测中是如何考查的,以及是否有新考法出现。
先了解一下,等差数列的基础内容,等差数列是指从第二项起,每一项与它的前一项的差等于一个常数的数列,一般我们用表示第1项,表示第n项,表示公差,常考点有两个,第一个是等差数列的通项公式:,第二个就是等差数列的前n项和公式:。通常考法就是单纯考查公式,那让我们来看一下在国考中会如何出题。
【例1】某种产品每箱48个。小李制作这种产品,第1天制作了1个,以后每天都比前一天多制作1个。天后总共制作了整数箱产品。问的最小值在以下哪个范围内?()
【解析】根据题目条件可知,小李制作这种产品X天,每天制作量分别为1,2,3,鈥︹��,X为一组公差为1的等差数列,其和为,要使其为整数且每箱48个,我们并不知道最终生产了多少箱,那么可以设生产Y箱,可列式为:,这里我们有两个未知数,但是只有一个方程,直接求解明显是做不到的,但是进一步分析,我们可知X、Y均为正整数,那么将等式变形为:,注意到(X+1)X必然是一奇一偶的两个数相乘,故只需分解96使得其为一奇一偶相乘形式即可,能分解成1脳96或者3脳32,由于求X的最小值,但是X在10以内明显不能满足条件,那么就可以使得X+1=32或X=32,若X=31,Y并不是整数,不成立,若X=32,Y=11成立,故X最小值为32,选择D选项。
【总结】国考中考到等差数列,并不是单纯的考查公式,而且将其与其他知识点结合,就像上述题目,就是把等差数列与最值问题结合,通过等差数列求前n项和,接着通过列式以及未知数的性质进行分析求解最值,难度要比单纯考查等差数列高不少,很是考查考生对于基本知识点的掌握和理解,这也是近几年国考行测很喜欢考查的内容,就是数理分析能力。同年,还出了另一道有关等差数列的题目
【例2】某种糖果的进价为12元/千克,现购进这种糖果若干千克,每天销售10千克,且从第二天起每天都比前一天降价2元/千克。已知以6元/千克的价格销售的那天正好卖完最后10千克,且总销售额是总进货成本的2倍。问总共进了多少千克这种糖果?()
【解析】根据题目条件和问题,由于每天都销售10千克的糖果,要求总共进了多少糖果就是要求共售卖了多少天,然而题目中除了销售情况外并无其他关于天数的条件,那么只能设售卖了x天,接着分析题目可知,有进价无初始售价,有最终售价以及每天售价的变化,由于售价每天递减2元,这明显是一个等差数列,但是不知道初始售价,需要反推,这里不推荐大家运用这个思路,我们可以这么想,把销售情况倒着看,那么就是初始售价为6元,每天递增2元的等差数列,共售卖x天,此时每天售价就很容易表示,分别为6,8,10,鈥︹��,6+2(x-1),在根据"总销售额是总进货成本的2倍"可列式为:,解得:x=19,总共进了19脳10=190千克糖果。
【总结】这道题就是等差数列结合了经济利润问题的考法,而且当等差数列是递减的且知道最后一项时,不建议通过通项公式去反向首项,可以将其看成把最后一项当成第一项的递推数列,就符合正常的认知,做起来也得心应手许多,毕竟这么看才更加符合正常的认知。
综上所述,国考在考查等差数列的时候,会结合其他知识一起进行考查,比如结合最值问题以及经济利润问题,当然不止这两个可以,其他问题,诸如几何问题、日期星期问题、年龄问题等都可以和等差数列结合考查,但是无论如何结合,等差数列的基本知识都会考查到,大家一定要能熟练记忆和运用其通项公式和前n项和公式,方能笑傲考场!
 U633687664
U633687664
 U582121265
U582121265