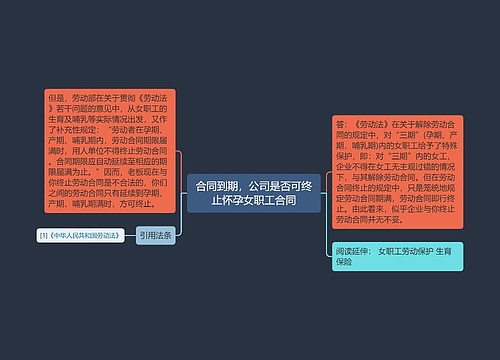
相信大家对赋值法已经很熟悉了，赋值法在很多题型中都有所应用，今天我们就来聊一聊赋值法如何更好的运用在经济利润问题中。
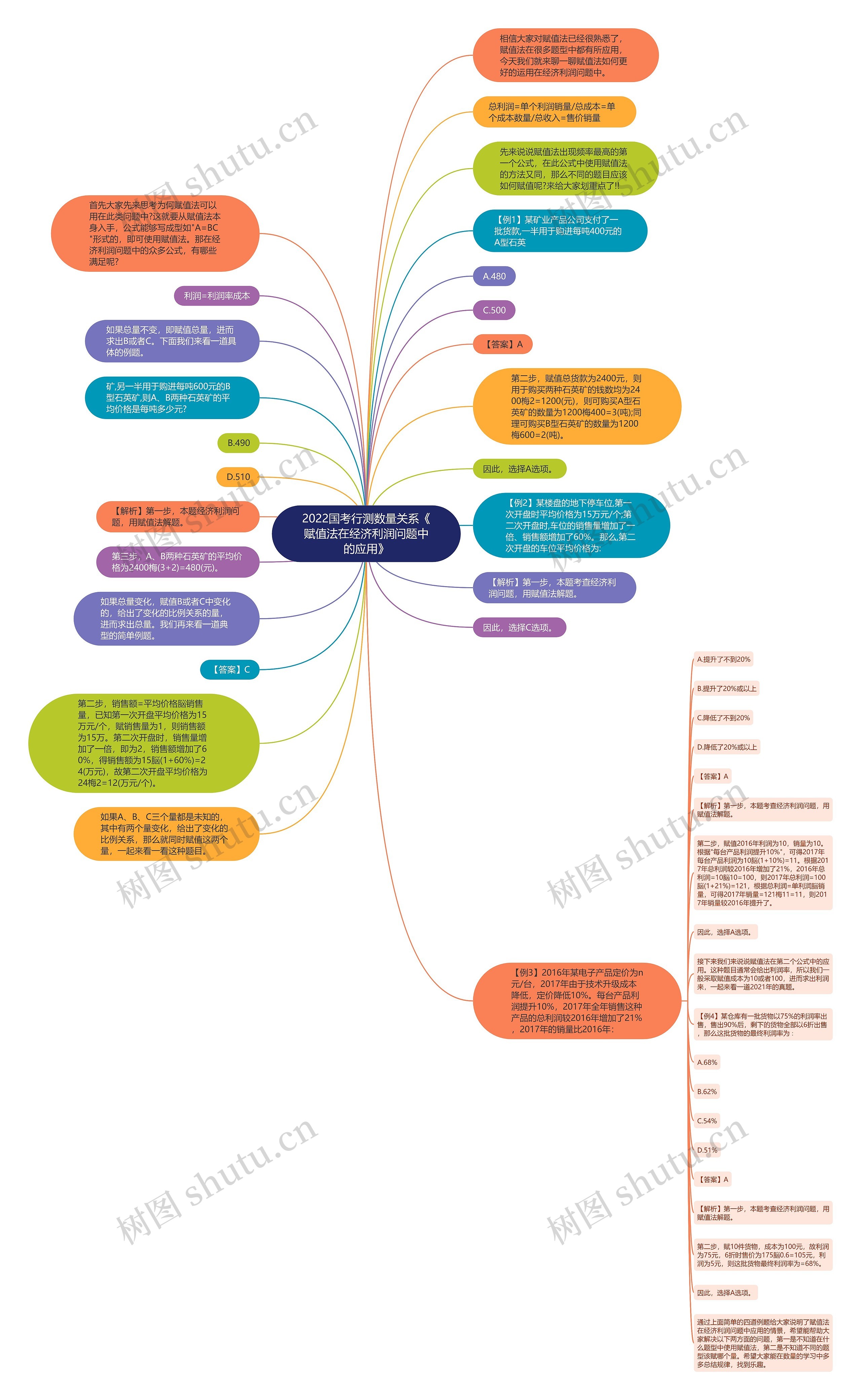
首先大家先来思考为何赋值法可以用在此类问题中?这就要从赋值法本身入手，公式能够写成型如"A=BC"形式的，即可使用赋值法。那在经济利润问题中的众多公式，有哪些满足呢?
总利润=单个利润销量/总成本=单个成本数量/总收入=售价销量
先来说说赋值法出现频率最高的第一个公式，在此公式中使用赋值法的方法又同，那么不同的题目应该如何赋值呢?来给大家划重点了!!
如果总量不变，即赋值总量，进而求出B或者C。下面我们来看一道具体的例题。
【例1】某矿业产品公司支付了一批货款,一半用于购进每吨400元的A型石英
矿,另一半用于购进每吨600元的B型石英矿,则A、B两种石英矿的平均价格是每吨多少元?
第二步，赋值总货款为2400元，则用于购买两种石英矿的钱数均为2400梅2=1200(元)，则可购买A型石英矿的数量为1200梅400=3(吨);同理可购买B型石英矿的数量为1200梅600=2(吨)。
第三步，A、B两种石英矿的平均价格为2400梅(3+2)=480(元)。
如果总量变化，赋值B或者C中变化的，给出了变化的比例关系的量，进而求出总量。我们再来看一道典型的简单例题。
【例2】某楼盘的地下停车位,第一次开盘时平均价格为15万元/个;第二次开盘时,车位的销售量增加了一倍、销售额增加了60%。那么,第二次开盘的车位平均价格为:
【解析】第一步，本题考查经济利润问题，用赋值法解题。
第二步，销售额=平均价格脳销售量，已知第一次开盘平均价格为15万元/个，赋销售量为1，则销售额为15万。第二次开盘时，销售量增加了一倍，即为2，销售额增加了60%，得销售额为15脳(1+60%)=24(万元)，故第二次开盘平均价格为24梅2=12(万元/个)。
如果A、B、C三个量都是未知的，其中有两个量变化，给出了变化的比例关系，那么就同时赋值这两个量，一起来看一看这种题目。
【例3】2016年某电子产品定价为n元/台，2017年由于技术升级成本降低，定价降低10%。每台产品利润提升10%，2017年全年销售这种产品的总利润较2016年增加了21%，2017年的销量比2016年：
【解析】第一步，本题考查经济利润问题，用赋值法解题。
第二步，赋值2016年利润为10，销量为10。根据"每台产品利润提升10%"，可得2017年每台产品利润为10脳(1+10%)=11。根据2017年总利润较2016年增加了21%，2016年总利润=10脳10=100，则2017年总利润=100脳(1+21%)=121，根据总利润=单利润脳销量，可得2017年销量=121梅11=11，则2017年销量较2016年提升了。
接下来我们来说说赋值法在第二个公式中的应用。这种题目通常会给出利润率，所以我们一般采取赋值成本为10或者100，进而求出利润来，一起来看一道2021年的真题。
【例4】某仓库有一批货物以75%的利润率出售，售出90%后，剩下的货物全部以6折出售，那么这批货物的最终利润率为∶
【解析】第一步，本题考查经济利润问题，用赋值法解题。
第二步，赋10件货物，成本为100元，故利润为75元，6折时售价为175脳0.6=105元，利润为5元，则这批货物最终利润率为=68%。
通过上面简单的四道例题给大家说明了赋值法在经济利润问题中应用的情景，希望能帮助大家解决以下两方面的问题，第一是不知道在什么题型中使用赋值法，第二是不知道不同的题型该赋哪个量。希望大家能在数量的学习中多多总结规律，找到乐趣。
U170141402
Kar.Logic
