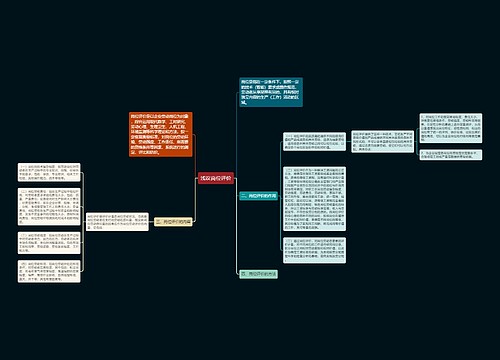
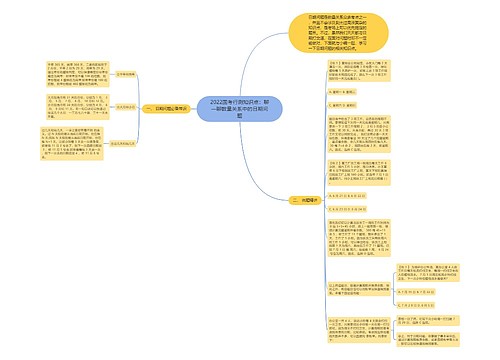
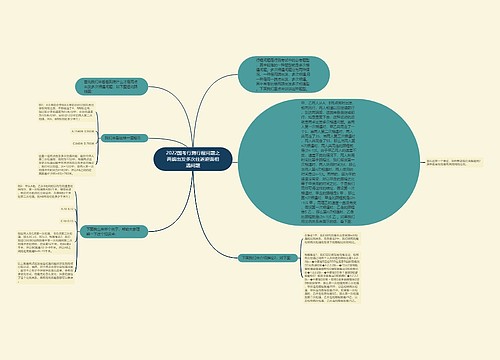
国考2022行测数量关系知识点:植树问题思维导图
补偿
2023-03-03

在公务员考试的战场上,怎样才能在 数量关系 部分发挥出色呢?答案只有一个:扎实掌握历年考试中经常出现的数学知识点!心中有干货,下手不慌张,奉劝各位正在备考的同学,不要再执着于学习五花八门的奇淫巧技,与其花大量时间研究各种野路子
树图思维导图提供《国考2022行测数量关系知识点:植树问题》在线思维导图免费制作,点击“编辑”按钮,可对《国考2022行测数量关系知识点:植树问题》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4417fead63e6838b60d82b35cfac68b9
思维导图大纲
相关思维导图模版
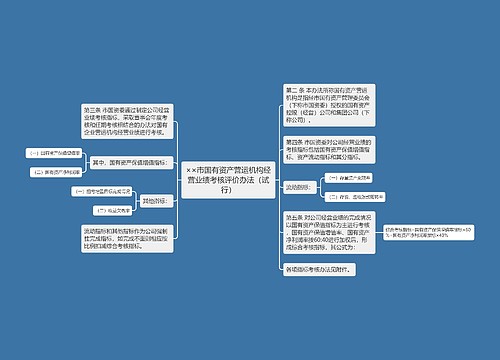
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
 U633687664
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作,点击“编辑”按钮,可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

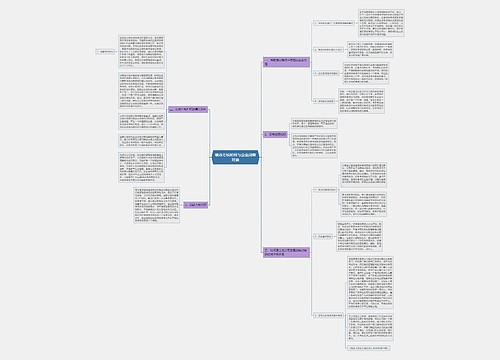
抓住重点思维导图
 ~漫埗陽茪~
~漫埗陽茪~树图思维导图提供《抓住重点》在线思维导图免费制作,点击“编辑”按钮,可对《抓住重点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826