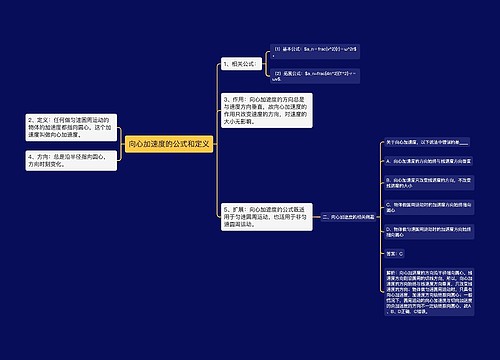
水平面内圆周运动的模型和临界问题思维导图
心不动则不痛
2023-01-12

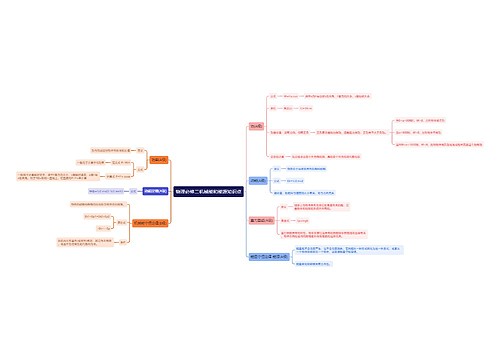
一、水平面内圆周运动的模型和临界问题
树图思维导图提供《水平面内圆周运动的模型和临界问题》在线思维导图免费制作,点击“编辑”按钮,可对《水平面内圆周运动的模型和临界问题》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:23ff14c8d184fba2f91f8c54c5d5aa91
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
 U633687664
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作,点击“编辑”按钮,可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

光和影思维导图
 小包卡麻麻
小包卡麻麻树图思维导图提供《光和影》在线思维导图免费制作,点击“编辑”按钮,可对《光和影》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2f4c9606f70a3f8d98ec4d65695dc3d1