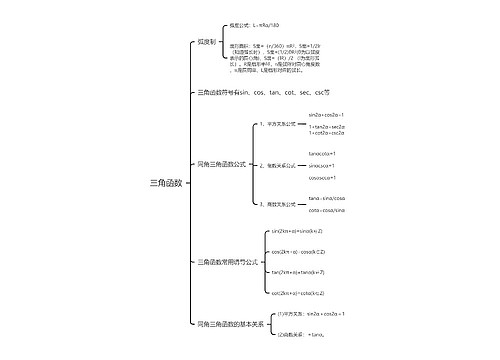
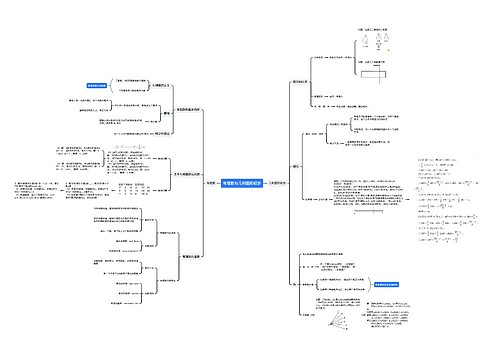
（1）整体解题策略是1求导去正（常见通分去恒正分母，提取去恒正指数）求根（即导数图像的交点，也为极值点）；2分类讨论（开口、斜率，根存在、大小，定义域）；3作导数图看正负写单调区间。
（2）如果导数为二次函数，最重要的为两种导数根的讨论（大小性与存在性）：
（i）如果求根时不能因式分解，需要套求根公式（或者没有一次项的二次情况需要移项开方），这种根称之为无理根，无理根讨论其存在性，被开方数（即德尔塔）大于零则根存在，画导数图像出现两个交点，图像正负看图可得；如果被开方数小于等于零，根不存在或两根相等，画导数图像可知导数恒正（开口向下则恒负）。讨论存在性分两类。
（ii）如果求根时能因式分解，需要十字相乘得根（或者没有常数项的二次情况需要提取x因式分解），这种根称之为有理根，有理根讨论大小性；两根不等的两类，画导数图像出现两个交点，图像正负看图可得；如果两根相等，画导数图像可知导数恒正（开口向下则恒负）。讨论大小性分三类。
（4）求单调区间难点在于，如果开口、斜率，根存在、大小，定义域有多件事情需要讨论，会难度较大，此时的解决方案为求出分界点，采用分界点法进行分类讨论。
（1）整体解题策略，可以看做是求单调区间的延续，先讨论单调性，然后利用单调性换原原函数图像，最后数形结合求出最值。
（2）区间最值其中一个难点是出现了"区间"作为函数的人为定义域，所以需要讨论定义域。另外在人为定义域"区间"下，有些题目还可以增加求导去正的可能性。
（3）区间最值，在得到原函数图像后，可能会出现比大小的讨论。比大小的讨论会出现在两种情景中。
（i）如果得到区间内图象为"V"型的单极值函数图象，求最大值则需比较端点函数的大小（倒"V"型则相似）
（ii）如果得到区间内图象为"N"型的双极值函数图象，无论求最大值还是最小值都需要比较一侧端点值与极值的大小。
（1）不等式问题可以理解为区间最值的延续，不等式成立，转化最值成立，求出最值后代入不等式，求解不等式解出参数即可，注意最终整合时候的先交后并，注意任意存在所求最值不一样，从理解角度出发并无太大难处。
（2）不等式成立的有些题目可能需要变形，有些题目需要变形后在求最值，常见变形包含：双侧单个变量的移项到一侧的变形，化简变形，参变分离变形。
（3）不等式成立题目处理有时可以理解为两个图象的几何意义，有时候称之为转化初等函数法。
（4）不等式成立题目在求最值的时候，如果遇见比大小的题目往往不需要比较大小，因为我们只需使得不等式成立即可，这样的话可以让需比较大小的函数值都成立"取交集"（任意型不等式），或成立"取并集"（存在型不等式）
（1）方程根等价于移项到一侧的函数零点，等价于图像与x轴交点（有时也可以理解为垂直于y轴的直线的交点），所以实根分布问题可以看做是问题一求单调区间的另一种延续，先求导讨论单调性，然后画出原函数图像，按照数形结合的思想使得极值与端点值异号，从图中即可发现根、零点分布成立了。
（2）根、零点的问题类似于不等式成立的问题，有可能需要变形，有些题目需要变形后在求单调性作图，双侧单个变量的移项到一侧的变形，化简变形，参变分离变形。
（3）根、零点的问题类似于不等式成立的问题，处理有时可以理解为两个图象的几何意义，有时候称之为转化初等函数法。
（4）由于不等式成立还可以理解为函数 图像在x轴上方或下方，某些不等式的题目也可以采用实根分布的做法来求解。
