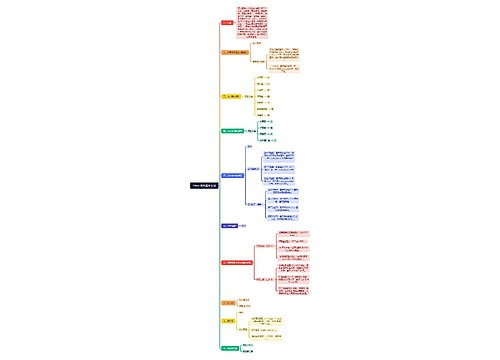
函数思维导图模板大纲
初等(基础)函数:一次函数、二次函数、反比例函数的图像与性质。
基本初等函数:指数函数、对数函数、幂函数的定义、图像、单调性、奇偶性等。
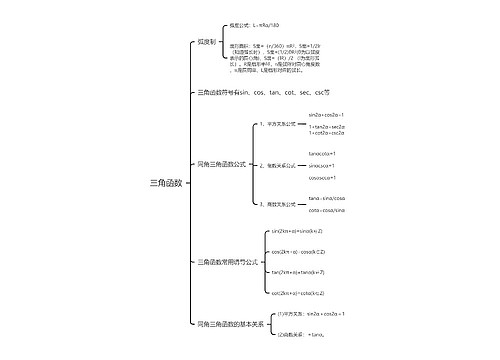
三角函数:正弦函数、余弦函数、正切函数的图像、性质、三角恒等变换(如两角和差公式、二倍角公式),以及解三角形(正弦定理、余弦定理的应用)
函数的通用性质:定义域、值域、单调性、奇偶性、周期性等。思维导图模板大纲
基础函数与基本初等函数的区别思维导图模板大纲
“初等” 二字的意义:明确数学上的 “基本单元”
“初等” 在这里强调的是它们的 “不可再分性”—— 是构成其他所有函数的最小单位,就像化学中的 “元素” 是构成物质的基本单元一样。
数学中对 “基本初等函数” 有严格定义:仅包括幂函数、指数函数、对数函数、三角函数、反三角函数五类(常数函数可视为特殊的幂函数(y=x⁰)。
“基础函数” 的命名更侧重 “学习阶段的基础性”(入门级、简单易懂),不涉及严格的数学定义,更多是教学中的通俗分类。
简单说:基本初等函数是 “原材料”,基础函数中的一次、二次函数是 “用原材料加工后的简单成品”
一次函数y=kx=+b二次函数ax²+bx+c是基本初等函数(幂函数)经过 “四则运算” 得到的
由基本初等函数经过有限次四则运算或复合得到的函数叫初等函数思维导图模板大纲
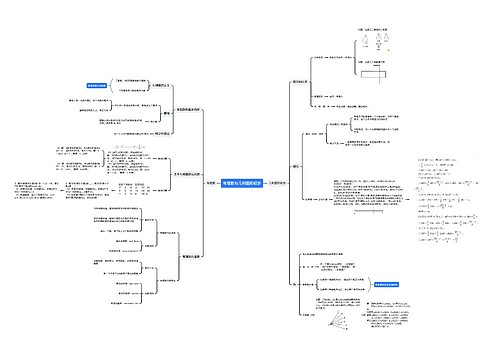
函数(基础函数、基本初等函数、三角函数)是所有章节的 “原点”思维导图模板大纲
方程
方程可视为 “函数值为 0 时的特殊情况”(如方程f(x)=0的解就是函数y=f(x)的零点)
不等式
可视为 “函数值与 0 的大小关系”(如f(x)>0)的解集对应函数图像在 x 轴上方的部分)
数列“特殊的函数”
(定义域为正整数集的函数,通项公式f(+)=a₊本质是函数表达式)
导数“研究函数性质的高级工具”思维导图模板大纲
通过导数判断函数的单调性、极值,是对函数研究的深化
方程与函数很像,他们有什么区别吗?思维导图模板大纲
两者的定义与核心
是含有未知数的等式(如2x + 3 = 7,x² - 5x + 6 = 0),核心是 “寻求使等式成立的未知数的值”(即解)。它更像一个 “问题”,关注的是 “哪些数值能满足这个等式”。
是两个非空数集之间的对应关系(如y = 2x + 3,y = x²,)核心是 “变量之间的依赖关系”—— 对于自变量x的每一个取值,因变量y有唯一确定的值与之对应。它更像一个 “规则”,关注的是 “变量如何随着另一个变量变化”。
变量的角色
变量有明确的 “自变量” 和 “因变量” 之分。变量的关系是 “主动与被动” 的依赖关系,关注的是变化规律(如x变化时y如何变)
表现形式与用途
方程的表现形式是 “等式”,用途是 “求解具体数值”(如求方程的根)
函数的表现形式是 “对应关系”用途是 “描述变化规律”(如用二次函数描述抛物线运动的高度与时间的关系),结果是变量之间的整体关系,而非单个数值。
两者的联系在于:函数y = f(x)的零点(即f(x) = 0就是方程(f(x) = 0)的解,但这只是函数的一个 “特殊状态”,而非函数的全部。思维导图模板大纲

 U633687664
U633687664
 U880113127
U880113127