目录思维导图
玖月
2025-07-02

机器学习优化方法
如果某个特征当中有
如果某个特征当中有
梯度下降法、共轭梯度法、拟牛顿法等内容详述
树图思维导图提供《目录》在线思维导图免费制作,点击“编辑”按钮,可对《目录》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:69a85188b06970cda6f1dc28f2ea9bc6
思维导图大纲
相关思维导图模版
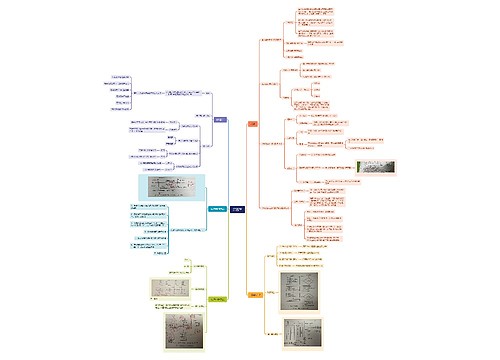
目录思维导图模板大纲
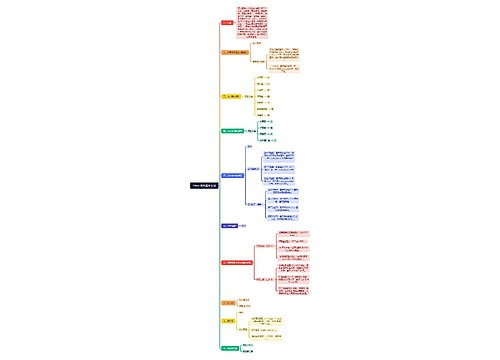
2. 机器学习优化方法
2.2 什么是凸优化
2.3 正则化项
2.4 常见的几种最优化方法
2.5 降维方法
2.1 机器学习常用损失函数
1. 特征工程有哪些?
1.2 类别型特征
1.3 高维组合特征的处理
1.4 文本表示模型
1.5 其它特征工程
1.6 特征工程脑图
1.1 特征归一化
1. 特征工程有哪些?
特征工程,顾名思义,是对原始数据进行一系列工程处理,将其提炼为特征,作为输入供算法和模型使用。从本质上来讲,特征工程是一个表示和展现数 据的过程。在实际工作中,
主要讨论以下两种常用的数据类型。
结构化数据。结构化数据类型可以看作关系型数据库的一张表,每列都 有清晰的定义,包含了数值型、类别型两种基本类型;每一行数据表示一个样本 的信息。
非结构化数据。非结构化数据主要包括文本、图像、音频、视频数据, 其包含的信息无法用一个简单的数值表示,也没有清晰的类别定义,并且每条数 据的大小各不相同。
1.1 特征归一化
为了消除数据特征之间的量纲影响,我们需要对特征进行归一化处理,使得 不同指标之间具有可比性。例如,分析一个人的身高和体重对健康的影响,如果 使用米(m)和千克(kg)作为单位,那么身高特征会在1.6~1.8m的数值范围 内,体重特征会在50~100kg的范围内,分析出来的结果显然会倾向于数值差别比 较大的体重特征。想要得到更为准确的结果,就需要进行特征归一化 (Normalization)处理,使各指标处于同一数值量级,以便进行分析。
对数值类型的特征做归一化可以将所有的特征都统一到一个大致相同的数值 区间内。最常用的方法主要有以下两种。
https://latex.codecogs.com/gif.latex?X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}}
https://latex.codecogs.com/gif.latex?z=\frac{x-u}{\sigma}
零均值归一化
Z
线性函数归一化
M
X
原
https://latex.codecogs.com/gif.latex?X_{max}、X_{min}
别
优点:
https://camo.githubusercontent.com/bf827828458d0f97939b34a216d9261ac42a79ff8807e2c6348009d2500f49fb/687474703a2f2f7778342e73696e61696d672e636e2f6d773639302f30303633304465666c7931673563646c343475626a6a3330677a30386934306a2e6a7067
当然,数据归一化并不是万能的。在实际应用中,通过梯度下降法求解的模 型通常是需要归一化的,包括线性回归、逻辑回归、支持向量机、神经网络等模 型。但对于决策树模型则并不适用。
1.2 类别型特征
类别型特征(Categorical Feature)主要是指性别(男、女)、血型(A、B、 AB、O)等只在有限选项内取值的特征。类别型特征原始输入通常是字符串形 式,除了决策树等少数模型能直接处理字符串形式的输入,对于逻辑回归、支持 向量机等模型来说,类别型特征必须经过处理转换成数值型特征才能正确工作。
序号编码通常用于处理类别间具有大小关系的数据。例如成绩,可以分为 低、中、高三档,并且存在“高>中>低”的排序关系。序号编码会按照大小关系对 类别型特征赋予一个数值ID,例如高表示为3、中表示为2、低表示为1,转换后依 然保留了大小关系。
独热编码通常用于处理类别间不具有大小关系的特征。例如血型,一共有4个 取值(A型血、B型血、AB型血、O型血),独热编码会把血型变成一个4维稀疏 向量,A型血表示为(1, 0, 0, 0),B型血表示为(0, 1, 0, 0),AB型表示为(0, 0, 1, 0),O型血表示为(0, 0, 0, 1)。对于类别取值较多的情况下使用独热编码。
独热编码(one-hot)
二进制编码主要分为两步,先用序号编码给每个类别赋予一个类别ID,然后 将类别ID对应的二进制编码作为结果。以A、B、AB、O血型为例,下图是二进制编码的过程。A型血的ID为1,二进制表示为001;B型血的ID为2,二进制表示为 010;以此类推可以得到AB型血和O型血的二进制表示。
https://camo.githubusercontent.com/2a99730a15a4c89cb52c0b8f7e019518d7aadac98dad2785a9c4fd43452bb011/687474703a2f2f7778312e73696e61696d672e636e2f6d773639302f30303633304465666c793167356364717a347a72756a33306c663037643734672e6a7067
二进制编码
序号编码
1.3 高维组合特征的处理
为了提高复杂关系的拟合能力,在特征工程中经常会把一阶离散特征两两组 合,构成高阶组合特征。以广告点击预估问题为例,原始数据有语言和类型两种 离散特征,第一张图是语言和类型对点击的影响。为了提高拟合能力,语言和类型可 以组成二阶特征,第二张图是语言和类型的组合特征对点击的影响。
https://camo.githubusercontent.com/ef92516998b46d02d1103bcef6f22b145208e97b99844e7f815793a10f665bd3/687474703a2f2f7778332e73696e61696d672e636e2f6d773639302f30303633304465666c7931673563647662756131616a33306e33306b663735322e6a7067
1.4 文本表示模型
文本是一类非常重要的非结构化数据,如何表示文本数据一直是机器学习领 域的一个重要研究方向。
最基础的文本表示模型是词袋模型。顾名思义,就是将每篇文章看成一袋子 词,并忽略每个词出现的顺序。具体地说,就是将整段文本以词为单位切分开, 然后每篇文章可以表示成一个长向量,向量中的每一维代表一个单词,而该维对 应的权重则反映了这个词在原文章中的重要程度。常用TF-IDF来计算权重。
主题模型用于从文本库中发现有代表性的主题(得到每个主题上面词的分布 特性),并且能够计算出每篇文章的主题分布。
主题模型
词嵌入是一类将词向量化的模型的统称,核心思想是将每个词都映射成低维 空间(通常K=50~300维)上的一个稠密向量(Dense Vector)。K维空间的每一 维也可以看作一个隐含的主题,只不过不像主题模型中的主题那样直观。
词嵌入与深度学习模型
词袋模型和N-gram模型
1.5 其它特征工程
如果某个特征当中有
可以分析特征与结果的相关性,把相关性小的特征去掉。
1.6 特征工程脑图
https://julyedu-img-public.oss-cn-beijing.aliyuncs.com/Public/Image/Question/1512980743_407.png
2. 机器学习优化方法
优化是应用数学的一个分支,也是机器学习的核心组成部分。实际上,机器 学习算法 = 模型表征 + 模型评估 + 优化算法。其中,优化算法所做的事情就是在 模型表征空间中找到模型评估指标最好的模型。不同的优化算法对应的模型表征 和评估指标不尽相同。
2.1 机器学习常用损失函数
损失函数(loss function)是用来估量你模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。常见的损失函数如下:
https://camo.githubusercontent.com/cfc03260facf99d602bc1a581b5f82b223f08834ec065cecafad563f5c993e50/687474703a2f2f7778312e73696e61696d672e636e2f6d773639302f30303633304465666c793167356535747a636769736a333061613031687765642e6a7067
Y-f(X)表示的是残差,整个式子表示的是残差的平方和,而我们的目的就是最小化这个目标函数值(注:该式子未加入正则项),也就是最小化残差的平方和。而在实际应用中,通常会使用均方差(MSE)作为一项衡量指标,公式如下:
https://latex.codecogs.com/gif.latex?MSE=\frac{1}{n}\sum_{i=1}^{n}(Y_i^{'}-Y_i
2
该损失函数一般使用在线性回归当中。
https://camo.githubusercontent.com/b18628e3c0560281acd5e14f43ec09e3e6a507f18b16d60d72d9a1c9b26f1aae/68747470733a2f2f7778312e73696e61696d672e636e2f6c617267652f30303633304465666c793167347076747a337477396a333065743034763073772e6a7067
公式中的 y=1 表示的是真实值为1时用第一个公式,真实 y=0 用第二个公式计算损失。为什么要加上log函数呢?可以试想一下,当真实样本为1是,但h=0概率,那么log0=∞,这就对模型最大的惩罚力度;当h=1时,那么log1=0,相当于没有惩罚,也就是没有损失,达到最优结果。所以数学家就想出了用log函数来表示损失函数。
最后按照梯度下降法一样,求解极小值点,得到想要的模型效果。该损失函数一般使用在逻辑回归中。
https://camo.githubusercontent.com/3ea05bfd4edbb5d91aa50d9c81a039158f530020d6683529fce4225ab4023a5e/687474703a2f2f7778322e73696e61696d672e636e2f6d773639302f30303633304465666c793167356366377a316b31726a3330623430623477656a2e6a7067
log损失函数
https://latex.codecogs.com/gif.latex?L_i=\sum_{j\neq t_i}max(0,f(x_i,W
j-(f(x
,
{y
}
SVM采用的就是Hinge Loss,用于“最大间隔(max-margin)”分类。
https://camo.githubusercontent.com/974d99c908d99779a18dd4b7eebbe0c3243497b575765a6cace2cd9c7a4d2b8f/687474703a2f2f7778312e73696e61696d672e636e2f6d773639302f30303633304465666c793167347735657a6a7236346a333073653033706d79362e6a7067
详细见之前
Hinge损失函数
平方损失函数
2.2 什么是凸优化
凸函数
严
https://camo.githubusercontent.com/7b8d336046f903f7db381c4725e930748465331541e94b2619ba30c18bcadd86/687474703a2f2f7778342e73696e61696d672e636e2f6d773639302f30303633304465666c7931673565357769736474756a333064343031696a72612e6a7067
该不等式的一个直观解释是,凸函数曲面上任意两点连接而成的线段,其上的任 意一点都不会处于该函数曲面的下方,如下图所示所示。
https://camo.githubusercontent.com/a1976e2d279dc4a46f9a4926f970ee59b77733064aa5978281364950d469f8a7/687474703a2f2f7778342e73696e61696d672e636e2f6d773639302f30303633304465666c793167356366706d7336776f6a3330653130343977657a2e6a7067
凸优化问题的例子包括支持向量机、线性回归等 线性模型,非凸优化问题的例子包括低秩模型(如矩阵分解)、深度神经网络模型等。
2.3 正则化项
使用正则化项,也就是给loss function加上一个参数项,正则化项有**L1正则化、L2正则化。加入这个正则化项好处:
控制参数幅度,不让模型“无法无天”。
限制参数搜索空间
解决欠拟合与过拟合的问题。
2.4 常见的几种最优化方法
梯度下降法是最早最简单,也是最为常用的最优化方法。梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。梯度下降法的搜索迭代示意图如下图所示:
https://images2017.cnblogs.com/blog/1022856/201709/1022856-20170916201932735-243646199.png
缺点:靠近极小值时收敛速度减慢;直线搜索时可能会产生一些问题;可能会“之字形”地下降。
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。具体步骤:
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标,也就是求如下方程的解:
https://latex.codecogs.com/gif.latex?x*f^{'}(x_0
f
0)-x
*
我们将新求得的点的 x 坐标命名为x1,通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。
https://images2017.cnblogs.com/blog/1022856/201709/1022856-20170916202719078-1588446775.gif
由于牛顿法是基于当前位置的切线来确定下一次的位置,所以牛顿法又被很形象地称为是"切线法"。牛顿法搜索动态示例图:
从本质上去看,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快。
牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
在高维情况下这个矩阵非常大,计算和存储都是问题。
在小批量的情况下,牛顿法对于二阶导数的估计噪声太大。
目标函数非凸的时候,牛顿法容易受到鞍点或者最大值点的吸引。
首先,选择一个接近函数 f (x)零点的 x0,计算相应的 f (x0) 和切线斜率f ' (x0)(这里f ' 表示函数 f 的导数)。
牛顿法
拟牛顿法是求解非线性优化问题最有效的方法之一,
拟牛顿法
共轭梯度法是介于梯度下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了梯度下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。 在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
具体的实现步骤请参加wiki百科
https://camo.githubusercontent.com/576212a69c4dac107ca56485b1e6689faab288b0d0f809a723257ab174af37a8/687474703a2f2f7778322e73696e61696d672e636e2f6d773639302f30303633304465666c7931673563683072327034386a3330387a30616c6d79342e6a7067
共轭梯度法
梯度下降法
2.5 降维方法
2.5.1 线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis,LDA)是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同,LDA是一种监督学习的降维技术,数据集的每个样本有类别输出。
LDA分类思想简单总结如下:
多维空间中,数据处理分类问题较为复杂,LDA算法将多维空间中的数据投影到一条直线上,将d维数据转化成1维数据进行处理。
对于训练数据,设法将多维数据投影到一条直线上,同类数据的投影点尽可能接近,异类数据点尽可能远离。
对数据进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定样本的类别。
如果用一句话概括LDA思想,
假设有红、蓝两类数据,这些数据特征均为二维,如下图所示。我们的目标是将这些数据投影到一维,让每一类相近的数据的投影点尽可能接近,不同类别数据尽可能远,即图中红色和蓝色数据中心之间的距离尽可能大。
https://camo.githubusercontent.com/e45edae3d77150c9677e3d41c22f30ca1e6b23e0dda4ca15b7a5840eb284c51a/687474703a2f2f7778342e73696e61696d672e636e2f6d773639302f303036333044656667793167356d613739756a706c6a33307172306163337a382e6a7067
左图和右图是两种不同的投影方式。
左图思路:让不同类别的平均点距离最远的投影方式。
右图思路:让同类别的数据挨得最近的投影方式。
从上图直观看出,右图红色数据和蓝色数据在各自的区域来说相对集中,根据数据分布直方图也可看出,所以右图的投影效果好于左图,左图中间直方图部分有明显交集。
以上例子是基于数据是二维的,分类后的投影是一条直线。如果原始数据是多维的,则投影后的分类面是一低维的超平面。
优缺点
| 优缺点 | 简要说明 |
| :----: | :----------------------------------------------------------- |
| 优点 | 1. 可以使用类别的先验知识;<br />2. 以标签、类别衡量差异性的有监督降维方式,相对于PCA的模糊性,其目的更明确,更能反映样本间的差异; |
| 缺点 | 1. LDA不适合对非高斯分布样本进行降维;<br />2. LDA降维最多降到分类数k-1维;<br />3. LDA在样本分类信息依赖方差而不是均值时,降维效果不好;<br />4. LDA可能过度拟合数据。 |
2.5.2 主成分分析(PCA)
PCA就是将高维的数据通过线性变换投影到低维空间上去。
投影思想:找出最能够代表原始数据的投影方法。被PCA降掉的那些维度只能是那些噪声或是冗余的数据。
去冗余:去除可以被其他向量代表的线性相关向量,这部分信息量是多余的。
去噪声,去除较小特征值对应的特征向量,特征值的大小反映了变换后在特征向量方向上变换的幅度,幅度越大,说明这个方向上的元素差异也越大,要保留。
对角化矩阵,寻找极大线性无关组,保留较大的特征值,去除较小特征值,组成一个投影矩阵,对原始样本矩阵进行投影,得到降维后的新样本矩阵。
完成PCA的关键是——协方差矩阵。协方差矩阵,能同时表现不同维度间的相关性以及各个维度上的方差。协方差矩阵度量的是维度与维度之间的关系,而非样本与样本之间。
之所以对角化,因为对角化之后非对角上的元素都是0,达到去噪声的目的。对角化后的协方差矩阵,对角线上较小的新方差对应的就是那些该去掉的维度。所以我们只取那些含有较大能量(特征值)的维度,其余的就舍掉,即去冗余。
PCA
PCA可解决训练数据中存在数据特征过多或特征累赘的问题。核心思想是将m维特征映射到n维(n < m),这n维形成主元,是重构出来最能代表原始数据的正交特征。
假设数据集是m个n维,$(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \cdots, \boldsymbol x^{(m)})$。如果$n=2$,需要降维到$n'=1$,现在想找到某一维度方向代表这两个维度的数据。
两个主要评价指标:
样本点到这个直线的距离足够近。
样本点在这个直线上的投影能尽可能的分开。
如果我们需要降维的目标维数是其他任意维,则:
样本点到这个超平面的距离足够近。
样本点在这个超平面上的投影能尽可能的分开。
优缺点
| 优缺点 | 简要说明 |
| :----: | :----------------------------------------------------------- |
| 优点 | 1. 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。 2.各主成分之间正交,可消除原始数据成分间的相互影响的因素。3. 计算方法简单,主要运算是特征值分解,易于实现。 |
| 缺点 | 1.主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。2. 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。 |
2.5.3 比较这两种方法
降维的必要性
多重共线性和预测变量之间相互关联。多重共线性会导致解空间的不稳定,从而可能导致结果的不连贯。
高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间,而在十维空间上只有2%。
过多的变量,对查找规律造成冗余麻烦。
仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。
降维的目的
减少预测变量的个数。
确保这些变量是相互独立的。
提供一个框架来解释结果。相关特征,特别是重要特征更能在数据中明确的显示出来;如果只有两维或者三维的话,更便于可视化展示。
数据在低维下更容易处理、更容易使用。
去除数据噪声。
降低算法运算开销。
LDA和PCA区别
| 异同点 | LDA | PCA |
| :----: | :----------------------------------------------------------- | :--------------------------------- |
| 相同点 | 1. 两者均可以对数据进行降维;<br />2. 两者在降维时均使用了矩阵特征分解的思想;<br />3. 两者都假设数据符合高斯分布; | |
| 不同点 | 有监督的降维方法; | 无监督的降维方法; |
| | 降维最多降到k-1维; | 降维多少没有限制; |
| | 可以用于降维,还可以用于分类; | 只用于降维; |
| | 选择分类性能最好的投影方向; | 选择样本点投影具有最大方差的方向; |
| | 更明确,更能反映样本间差异; | 目的较为模糊; |
查看更多
证据目录思维导图
 U676683698
U676683698树图思维导图提供《证据目录》在线思维导图免费制作,点击“编辑”按钮,可对《证据目录》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:1bad2e32ffa6e69aece239ba270027a6

浙江省政府集中采购目录及标准(2023 年版)思维导图
 U774568524
U774568524树图思维导图提供《浙江省政府集中采购目录及标准(2023 年版)》在线思维导图免费制作,点击“编辑”按钮,可对《浙江省政府集中采购目录及标准(2023 年版)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a680ee8ce3ae477cc1793d0da635a1f8
相似思维导图模版
首页
我的文件
我的团队
个人中心