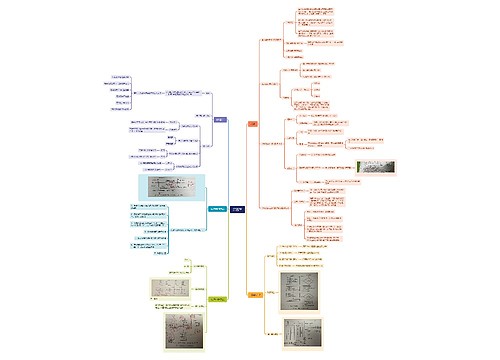
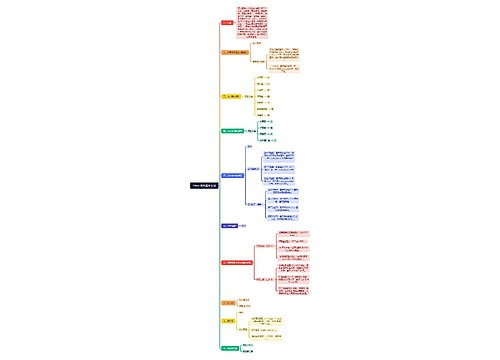
线性回归思维导图

玖月

2025-07-02

浏览量: 50

模型训练

正则化

计算均方误差

线性回归内容详述

树图思维导图提供《线性回归》在线思维导图免费制作，点击“编辑”按钮，可对《线性回归》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：5bf318261f3de7b2837ef15712554c31

思维导图大纲

线性回归介绍

学习目标：

1.理解线性回归是什么？

2.知道一元线性回归和多元线性回归的区别

3.知道线性回归的应用场景

【理解】举个栗子

假若有了身高和体重数据，来了播仔的身高，你能预测播仔体重吗?

这是一个回归问题，该如何求解呢?

思路

先

•数学问题：用一条线来拟合身高和体重之间的关系，再对新数据进行预测

方程 Y = kX + b

k160 + b = 56.3 -- (1)

k166 + b = 60.6 –- (2)

。。。。

k: 斜率 b:截距

若：y = 0.9 x + (-93)

0.9*176 +（-93）= ?

【理解】线性回归

线性回归(Linear regression)是利用

注意事项：

1 为什么叫线性模型？因为求解的w，都是w的零次幂（常数项）所以叫成线性模型

2 在线性回归中，从数据中获取的规律其实就是学习权重系数w

3 某一个权重值w越大，说明这个权重的数据对房子价格影响越大

【知道】线性回归分类

一元线性回归

y = kx +b

目标值只与一个因变量有关系

多元线性回归

目标值只与多个因变量有关系

线性回归问题的求解

学习目标：

1.知道线性回归API的使用

2.知道损失函数是什么

3.复习导数和矩阵的相关内容

4.理解正规方程法

5.掌握梯度下降算法的内容

【掌握】损失函数

需要设置一个评判标准

images/image-20230901110253313.png

损失函数

衡

“红色直线能更好的拟合所有点”也就是误差最小，误差和最小

损失函数数学如何表达呢？又如何求损失函数的最小值呢？

images/image-20230901110606206.png

images/image-20230901110842936.png

images/image-20230901110853094.png

当损失函数取最小值时，得到k就是最优解

images/image-20230901113810862.png

images/image-20230901113822728.png

images/image-20230901113834036.png

想求一条直线更好的拟合所有点 y = kx + b

通过一个优化方法，求损失函数最小值，得到K最优解

引入损失函数(衡量预测值和真实值效果) Loss(k, b)

images/image-20230912103729099.png

回归的损失函数：

均方误差

(

)

images/image-20230901114527268.png

images/image-20230901114539398.png

平均绝对误差

(**Mean Absolute Error

MAE**)

images/image-20230901114816872.png

【了解】一元线性回归的解析解

images/image-20230901150406897.png

images/image-20230901150708528.png

images/image-20230912145402703.png

【了解】多元线性回归的解析解-正规方程法

images/image-20230901152528805.png

images/image-20230911234116911.png

images/image-20230901152745308.png

images/image-20230901152758396.png

梯度下降算法

【掌握】梯度下降算法思想

什么是梯度下降法

• 求解函数极值还有更通用的方法就是梯度下降法。顾名思义:沿着梯度下降的方向求解极小值 • 举个例子:坡度最陡下山法

images/image-20230901183007785.png

输入:初始化位置S;每步距离为a 。输出:从位置S到达山底

步骤1:令初始化位置为山的任意位置S

步骤2:在当前位置环顾四周，如果四周都比S高返回S;否则执行步骤3

步骤3: 在当前位置环顾四周，寻找坡度最陡的方向，令其为x方向

步骤4:沿着x方向往下走，长度为a，到达新的位置S‘

步骤5:在S‘位置环顾四周，如果四周都比S‘高，则返回S‘。否则转到步骤3

小结:通过循环迭代的方法不断更新位置S (相当于不断更新权重参数w)

images/image-20230901183020726.png

最终找到最优解这个方法可用来求损失函数最优解，比正规方程更通用

梯度下降过程就和下山场景类似可微分的损失函数，代表着一座山寻找的函数的最小值，也就是山底

images/image-20230901183113930.png

images/image-20230901183125661.png

images/image-20230912163031832.png

images/image-20230901183139728.png

images/image-20230901183152966.png

【理解】银行信贷案例

images/image-20230901183222050.png

images/image-20230901183240178.png

images/image-20230901183301618.png

images/image-20230901183315009.png

【了解】梯度下降算法分类

images/image-20230901183333299.png

images/image-20230901183346878.png

【理解】正规方程和梯度下降算法的对比

images/image-20230901162716376.png

回归评估方法

学习目标：

1.掌握常用的回归评估方法

2.了解不同评估方法的特点

为什么要进行线性回归模型的评估

我们希望衡量预测值和真实值之间的差距，

会用到MAE、MSE、RMSE多种测评函数进行评价

【知道】平均绝对误差

Mean Absolute Error (MAE)

images/mae.png

MAE 越小模型预测约准确

上面的公式中：n 为样本数量, y 为实际值, $\hat{y}$ 为预测值

Sklearn 中MAE的API

python from sklearn.metrics import mean_absolute_error mean_absolute_error(y_test,y_predict)

【知道】均方误差

images/mse.png

上面的公式中：n 为样本数量, y 为实际值, $\hat{y}$ 为预测值

MSE 越小模型预测约准确

Sklearn 中MSE的API

python from sklearn.metrics import mean_squared_error mean_squared_error(y_test,y_predict)

【知道】均方根误差

Root Mean Squared Error (RMSE)

images/rmse.png

上面的公式中：n 为样本数量, y 为实际值, $\hat{y}$ 为预测值

RMSE 越小模型预测约准确

【了解】三种指标的比较

我们绘制了一条直线

images/rmse2.png

从上图中我们发现 MAE 和 RMSE 非常接近，都表明模型的误差很低（MAE 或 RMSE 越小，误差越小！）。但是MAE 和 RMSE 有什么区别？为什么MAE较低？

可以得出结论，RMSE 会放大预测误差较大的样本对结果的影响，而 MAE 只是给出了平均误差

由于 RMSE 对误差的

举例 (1+3)/2 = 2 $\sqrt{(1^2+3^2)/2 }= \sqrt{10/2} = \sqrt{5} = 2.236$

对比MAE 和 RMSE的公式，RMSE的计算公式中有一个平方项，因此：大的误差将被平方，因此会增加 RMSE 的值

我们再看下一个例子

images/rmse3.png

橙色线与第一张图中的直线一样：

蓝色的点为：

我们看到对比第一张图，所有的指标都变大了，RMSE 几乎是 MAE 值的两倍，因为它对预测误差较大的点比较敏感

我们是否可以得出结论： RMSE是更好的指标？某些情况下MAE更有优势，例如：

假设数据中有少数异常点偏差很大，如果此时根据 RMSE 选择线性回归模型，可能会选出过拟合的模型来

在这种情况下，由于数据中的异常点极少，选择具有最低 MAE 的回归模型可能更合适

除此之外，当两个模型计算RMSE时数据量不一致，也不适合在一起比较

【实操】波士顿房价预测案例

【知道】线性回归API

sklearn.linear

通过正规方程优化

参数：fit_intercept，是否计算偏置

属性：LinearRegression.coef

sklearn.linear

参数：loss（损失函数类型），fit

属性：SGDRegressor.coef

【实操】波士顿房价预测

images/image-20230913092037241.png

案例背景介绍

数据介绍

images/006tNbRwly1ga8u37zooxj317g0tc7dk.jpg

images/006tNbRwly1ga8u39xrmlj30xo0ryk16.jpg

给定的这些特征，是专家们得出的影响房价的结果属性。我们此阶段不需要自己去探究特征是否有用，只需要使用这些特征。到后面量化很多特征需要我们自己去寻找

案例分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。

数据分割与标准化处理

回归预测

线性回归的算法效果评估

回归性能评估

均方误差(Mean Squared Error, MSE)评价机制：

$\Large MSE = \frac{1}{m}\sum_{i=1}^{m}(y^i-\hat{y})^2$

sklearn中的API：sklearn.metrics.mean

均方误差回归损失

y_true:真实值

y_pred:预测值

return:浮点数结果

代码实现

0.导包

from sklearn.datasets import load

1.加载数据

boston = load_boston()

print(boston)

2.数据集划分

3.标准化

process=StandardScaler() x

4.模型训练

4.1 实例化(正规方程)

model =LinearRegression(fit_intercept=True)

model = SGDRegressor(learning_rate='constant',eta0=0.01)

4.2 fit

model.fit(x

print(model.coef_)

print(model.intercept_)

5.预测

print(y_predict)

6.模型评估

print(mean

1.2.0 以上版本实现

0.导包

from sklearn.datasets import load_boston

from sklearn.model

1.加载数据

boston = load_boston()

print(boston)

import pandas as pd import numpy as np

data

2.数据集划分

xtrain,xtest,y

3.标准化

process=StandardScaler() x

4.模型训练

4.1 实例化(正规方程)

model =LinearRegression(fit_intercept=True)

model = SGDRegressor(learning_rate='constant',eta0=0.01)

4.2 fit

model.fit(x

print(model.coef_)

print(model.intercept_)

5.预测

print(y_predict)

6.模型评估

print(mean

正则化

学习目标：

1.掌握过拟合、欠拟合的概念

2.掌握过拟合、欠拟合产生的原因

3.知道什么是正则化，以及正则化的方法

【理解】欠拟合与过拟合

过拟合：一个假设

欠拟合：一个假设

过拟合和欠拟合的区别：

欠拟合在训练集和测试集上的误差都较大

过拟合在训练集上误差较小，而测试集上误差较大

images/image-20230913101352444.png

【实践】通过代码认识过拟合和欠拟合

绘制数据

【理解】原因以及解决办法

欠拟合产生原因：

学

解决办法：

1）添加其他特征项

有

2）添加多项式特征

模

过拟合产生原因：

原

解决办法：

1）重新清洗数据，导致过拟合的一个原因有可能是数据不纯，如果出现了过拟合就需要重新清洗数据。

2）增大数据的训练量，还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小。

3）正则化

4）减少特征维度

【理解】正则化

在解决回归过拟合中，我们选择正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括之前说的删除、合并一些特征

如何解决？

在学习的时候，数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多，所以算法在学习的时候尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化

注：调整时候，算法并不知道某个特征影响，而是去调整参数得出优化的结

L1正则化

假设𝐿(𝑊)是未加正则项的损失，𝜆是一个超参，控制正则化项的大小。

则最终的损失函数：$𝐿=𝐿(𝑊)+ \lambda*\sum

作用：用来进行特征选择，主要原因在于L1正则化会使得较多的参数为0，从而产生稀疏解,可以将0对应的特征遗弃，进而用来选择特征。一定程度上L1正则也可以防止模型过拟合。

images/image-20230913145042318.png

L1正则为什么可以产生稀疏解（可以特征选择）

稀疏性：向量中很多维度值为0

对其中的一个参数 $ w_i $ 计算梯度，其他参数同理，α是学习率，sign(wi)是符号函数。

L1的梯度：

$𝐿=𝐿(𝑊)+ \lambda*\sum

$\frac{\partial L}{\partial w

LASSO回归: from sklearn.linear_model import Lasso

L2正则化

假设𝐿(𝑊)是未加正则项的损失，𝜆是一个超参，控制正则化项的大小。

则最终的损失函数：$𝐿=𝐿(𝑊)+ \lambda*\sum

作用：主要用来防止模型过拟合，可以减小特征的权重

优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象

Ridge回归: from sklearn.linear_model import Ridge

正则化案例

3,X

5,X

7,X

9,X

plt.scatter(x,y) plt.plot(np.sort(x),y_predict3[np.argsort(x)],color = 'r') plt.show()

estimator3.coef_

array([ 1.32292089e+00, 2.03952017e+00, -2.88731664e-01, -1.24760429e+00, 8.06147066e-02, 3.72878513e-01, -7.75395040e-03, -4.64121137e-02, 1.84873446e-04, 2.03845917e-03])

images/l2_5.png

model import Lasso # L1正则 from sklearn.linear

X10 = np.hstack([X2,X

plt.scatter(x,y) plt.plot(np.sort(x),y

estimator

array([ 0.97284077, 0.4850203 , 0. , 0. , -0. , 0. , -0. , 0. , -0. , 0. ])

images/l2_6.png

3,X

5,X

7,X

9,X

l2 = Ridge(alpha=0.005,normalize=True) # 调整alpha 正则化强度查看正则化效果 estimator

predict

plt.scatter(x,y) plt.plot(np.sort(x),y

estimator

array([ 9.91283840e-01, 5.24820573e-01, 1.57614237e-02, 2.34128982e-03, 7.26947948e-04, -2.99893698e-04, -8.28333499e-05, -4.51949529e-05, -4.21312015e-05, -8.22992826e-07])

images/l2_7.png