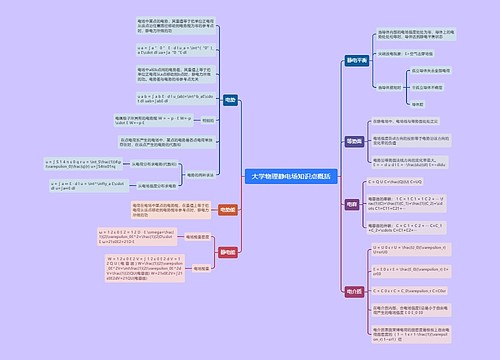
《大学物理学（第三版）》电磁学·波动光学·量子物理知识点汇编思维导图

U6101908976

2025-06-20

浏览量: 82

波动光学

衍射

《大学物理学（第三版）》电磁学·波动光学·量子物理知识点汇编内容详述

树图思维导图提供《《大学物理学（第三版）》电磁学·波动光学·量子物理知识点汇编》在线思维导图免费制作，点击“编辑”按钮，可对《《大学物理学（第三版）》电磁学·波动光学·量子物理知识点汇编》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：0fef6e5da523c7abd616639bdcc669c8

思维导图大纲

一、电磁学

静电场 → 电磁波；方法：对称性、积分定理、能量观点

1. 静电场

库仑定律：F = k |q₁q₂| / r²；矢量式 F⃗ = k q₁q₂ r̂ / r²

电场强度：E⃗ = F⃗ / q₀；叠加原理

场源方程：∇·E⃗ = ρ/ε₀ → 泊松方程 ∇²φ = −ρ/ε₀，真空静电场满足 ∇²φ = 0

高斯定理（积分）：∯_S E⃗·dS⃗ = Q_in / ε₀；常用：球、柱、无限大带电平面

边界条件：E_⊥ 上−下 = σ_f / ε₀， E_∥ 连续

电势：φ(P) = −∫_∞^P E⃗·dl⃗；等势面与场线正交

能量密度：u_e = ½ ε₀ E²；总能量 W = ½ ∭ ρ φ dV = ½ ε₀ ∭ E² dV

导体性质：静电平衡时内部 E⃗ = 0，表面电荷只分布在外表面；尖端放电 ∝ 1/R 曲率

像电荷法：带电球外电荷 → 像电荷 q' = − a q / r' 解决球面边界；带电平面镜像 q' = −q

电容：C = Q/U；典型—平板 C = ε₀ ε_r S/d，同心球 C = 4π ε₀ /(1/a − 1/b)

电极化：P⃗ = χ_e ε₀ E⃗；位移矢量 D⃗ = ε₀ E⃗ + P⃗ = ε E⃗

极化电荷：ρ_b = −∇·P⃗ ， σ_b = P⃗·n̂

2. 恒定电流与电路

电流密度 J⃗ = ρ_v v⃗；稳恒连续性 ∇·J⃗ = 0

欧姆定律 (微分) J⃗ = σ E⃗；宏观 U = IR

焦耳热功率密度 p = J⃗·E⃗ = ρ j²，导体发热 Q = I² R t

纯电阻-电感-电容网络：ΔV + L dI/dt + (1/C)∫ I dt = 0

3. 磁场与磁介质

毕奥-萨伐尔：dB⃗ = μ₀/4π · I (dl⃗ × r̂) / r²

直导线：B = μ₀ I / 2π r；圆环中心：B = μ₀ I / 2R

安培环路 ∮ B⃗·dl⃗ = μ₀ I_in；应用：无限长螺线管 B = μ₀ n I，托罗线圈 B = μ₀ N I / 2π r

洛伦兹力：F⃗ = q(E⃗ + v⃗ × B⃗)，电荷在匀强 B 中作圆运动 ω_c = qB/m

磁化：M⃗ = χ_m H⃗；边界条件 H_∥ 连续， B_⊥ 连续

束缚电流密度 J_b = ∇×M⃗ ，表面束缚 K_b = M⃗ × n̂

4. 电磁感应

法拉第感应定律：ℰ = − dΦ_B / dt ；积分型 ∮ E⃗·dl⃗ = − d/dt ∫ B⃗·dS⃗

楞次定律：感应电流方向阻碍磁通变化（能量守恒）

自感 L：Φ = L I；互感 M₁₂ = μ₀ N₁ N₂ S / l (匝耦合)

RL 暂态：I(t)=I₀(1 − e^{−t/τ}), τ = L/R

位移电流：J_d = ε₀ ∂E⃗/∂t ；修正安培定律

5. 交变电流与谐振

正弦电源：v(t)=V_m cos ωt； phasor V̂ = V_m/√2 ∠0°

阻抗：Z_R = R， Z_L = jω L， Z_C = 1/(jωC)

串联 RLC：总 Z = R + j(ωL − 1/ωC)，电流 Î = V̂ / Z

谐振：ω₀ = 1/√(LC)， I_max, Q = ω₀ L / R

功率：P = VI cosφ，无功 Q = VI sinφ， S = VI

δ = √(2 / ω μ σ)

6. 麦克斯韦方程与电磁波

微分形式：∇·E⃗=ρ/ε₀；∇·B⃗=0；∇×E⃗=−∂B⃗/∂t；∇×B⃗=μ₀J⃗+μ₀ε₀∂E⃗/∂t

真空波动方程：∇²E⃗ − (1/c²) ∂²E⃗/∂t² = 0； c = 1/√(μ₀ ε₀)

平面波：E⃗ = E₀ cos(k·r − ωt)， B⃗ = (1/ω) k̂ × E⃗

S⃗ = E⃗ × H⃗，平均能流密度 ⟨S⟩ = ½ Re(Ê × Ĥ*)

波阻抗：Z₀ = √(μ₀/ε₀) ≈ 377 Ω

界面反射：振幅反射系数 r = (n₁ − n₂)/(n₁ + n₂)；布鲁斯特角 tan θ_B = n₂/n₁

二、波动光学

相干 → 衍射 → 偏振 → 测量

1. 光的干涉

杨氏双缝强度：I = 4I₀ cos²(π d sinθ / λ)；条纹间距 Δy = λL/d

双筒透镜等厚干涉：2 n d cosθ = (m + ½) λ (反射)

迈克耳孙：光程差 2ΔL = mλ；用于测 λ、折射率 n

光程、相干长度：l_c = c τ_c = c/Δν

2. 光的衍射

单缝夫琅禾费：I = I₀ [sin(β)/β]², β = π a sinθ / λ

矩形孔二维：I = I₀ sinc²(β_x) sinc²(β_y)

衍射光栅：d sinθ = mλ；分辨率 R = mN；自由光谱范围 Δλ = λ/mN

菲涅耳数 N = a² / (λ L) 判别远近场

3. 光的偏振

马吕斯：I = I₀ cos²α

起偏片 → 波片 (λ/2, λ/4) → 分析镜，实现任意偏振态控制

双折射晶体：n_e ≠ n_o，相位差 Δφ = 2π (n_e − n_o) d / λ

旋光：φ = [α] c l；手性介质产生光学活性

4. 相干与全息

时间相干函数 γ(τ) = ⟨E(t) E*(t+τ)⟩ / ⟨|E|²⟩

空间相干取决于源大小：β ≈ D / (L λ)

激光全息：记录干涉条纹（物光+参考光）→ 重构波前获得 3D 图像

三、量子物理基础（下册）

实验 → 波粒二相性 → 量子力学理论（薛定谔方程等）

1. 量子化起源

普朗克假设：E = n h ν；黑体谱 u(ν) 公式

爱因斯坦光电方程：hν = W₀ + e V_s；截止频率 ν₀ = W₀ / h

康普顿散射：Δλ = h/(m_e c)(1 − cosθ)

波耳氢原子模型：m v r = n ħ；E_n = -13.6 eV / n²

2. 波粒二象性

德布罗意：λ = h/p；动量 p = ħ k

电子双缝实验：干涉条纹 λ = h/√(2 m e V)

3. 量子力学公设

态向量 |ψ⟩；几率密度 ρ = |ψ|²

算符 Â 线性厄米：⟨ψ|Â|ψ⟩ 实数

对易关系 [x̂, p̂_x] = iħ；最小不确定 Δx Δp ≥ ħ/2

薛定谔方程：iħ ∂ψ/∂t = Ĥ ψ；概率流 j = (ħ/2mi)(ψ*∇ψ − ψ∇ψ*)

4. 一维典型势

无限深势阱 0<x<L：ψ_n = √(2/L) sin(nπx/L), E_n = n²π²ħ²/2mL²

有限深势阱：束缚态由 κ tan κa = √(k₀² − κ²)

阶梯势：反射系数 R = |(k−q)/(k+q)|²

隧穿：T ≈ exp(−2κ a), κ = √(2m(U₀ − E))/ħ

简谐振子：Ĥ = p̂²/2m + ½ m ω² x²；能级 E_n = (n+½)ħω；â± 算符

5. 三维中心势 - 氢原子

径向方程：d²u/dr² + [2m/ħ²(E + e²/4π ε₀ r) − l(l+1)/r²]u = 0

能级：E_n = −13.6 eV / n²，简并度 n²

选择定则：Δl = ±1, Δm = 0, ±1 (电偶极辐射)

6. 自旋与多电子原子

自旋角动量 S = √(s(s+1))ħ；投影 S_z = m_s ħ

泡利不相容：全同费米子总波函数反对称

精细结构：自旋-轨道耦合 ΔE_fs ∝ α² Z⁴ / n³ (1/(j+½) − 3/4n)

北京鲁迅博物馆思维导图

U982669071

4.59

树图思维导图提供《北京鲁迅博物馆》在线思维导图免费制作，点击“编辑”按钮，可对《北京鲁迅博物馆》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：46dd5fb39ac0566fc4fa2033f0feb486

抓住重点思维导图

~漫埗陽茪~

3.13

树图思维导图提供《抓住重点》在线思维导图免费制作，点击“编辑”按钮，可对《抓住重点》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：4c49e4799ddf94a339c56e46eb96a826

思维导图模板

高校与高等教育

物理学

正文

相似思维导图模版

思维导图模版推荐

首页

我的文件

我的团队

个人中心

《大学物理学（第三版）》电磁学·波动光学·量子物理 知识点汇编思维导图