大学物理静电场知识点概括思维导图
U77418911
2022-10-04
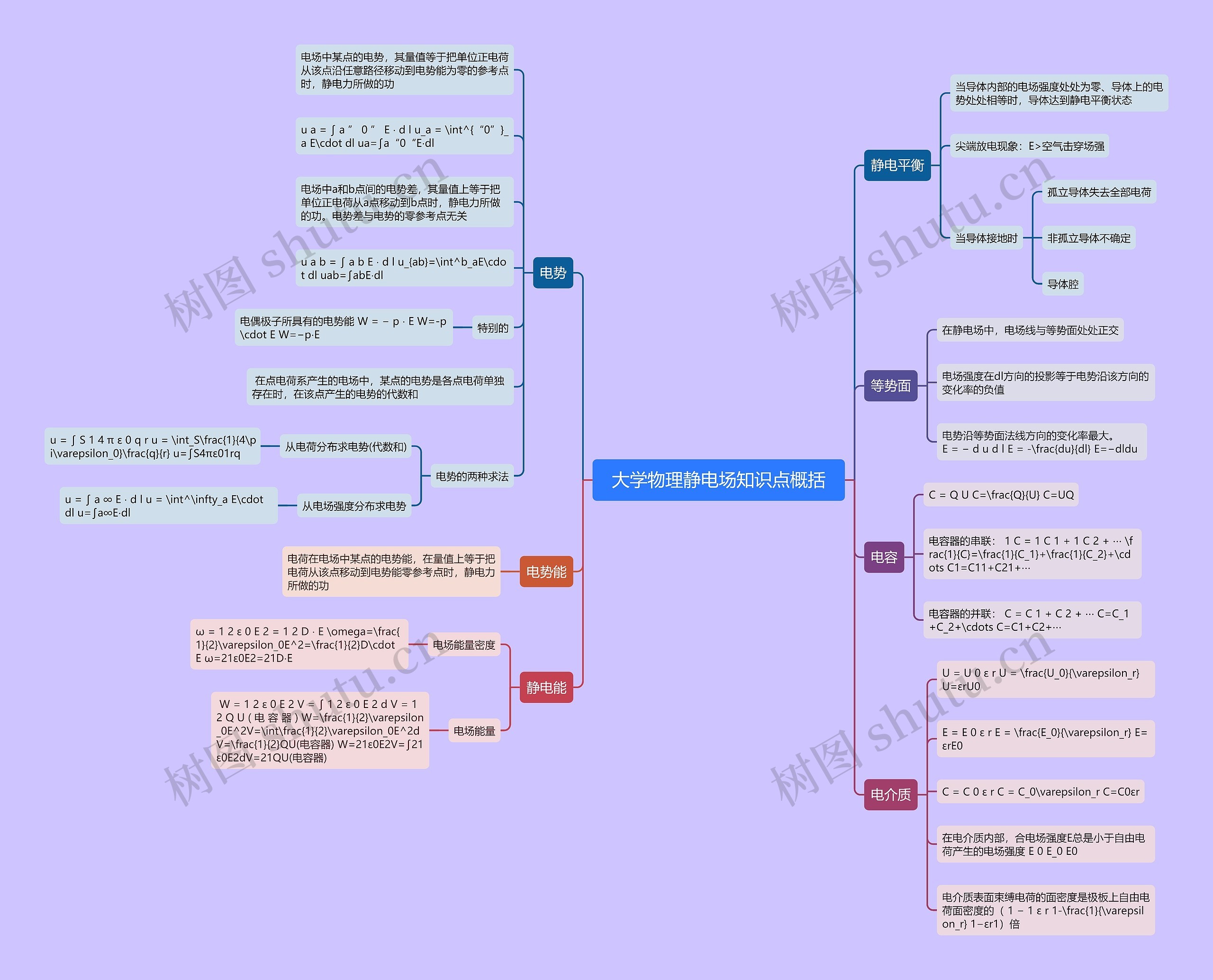
大学物理静电场知识点概括,电势、电势能、静电能、静电平衡、等势面、电容、电介质的知识点概括总结
树图思维导图提供《大学物理静电场知识点概括》在线思维导图免费制作,点击“编辑”按钮,可对《大学物理静电场知识点概括》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:bb52176c428d170e177cb7995bd7a4f1

大学物理静电场知识点概括,电势、电势能、静电能、静电平衡、等势面、电容、电介质的知识点概括总结
树图思维导图提供《大学物理静电场知识点概括》在线思维导图免费制作,点击“编辑”按钮,可对《大学物理静电场知识点概括》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:bb52176c428d170e177cb7995bd7a4f1