2020重庆国考数量关系公约数、公倍数总结思维导图
谎话最甜
2023-03-07
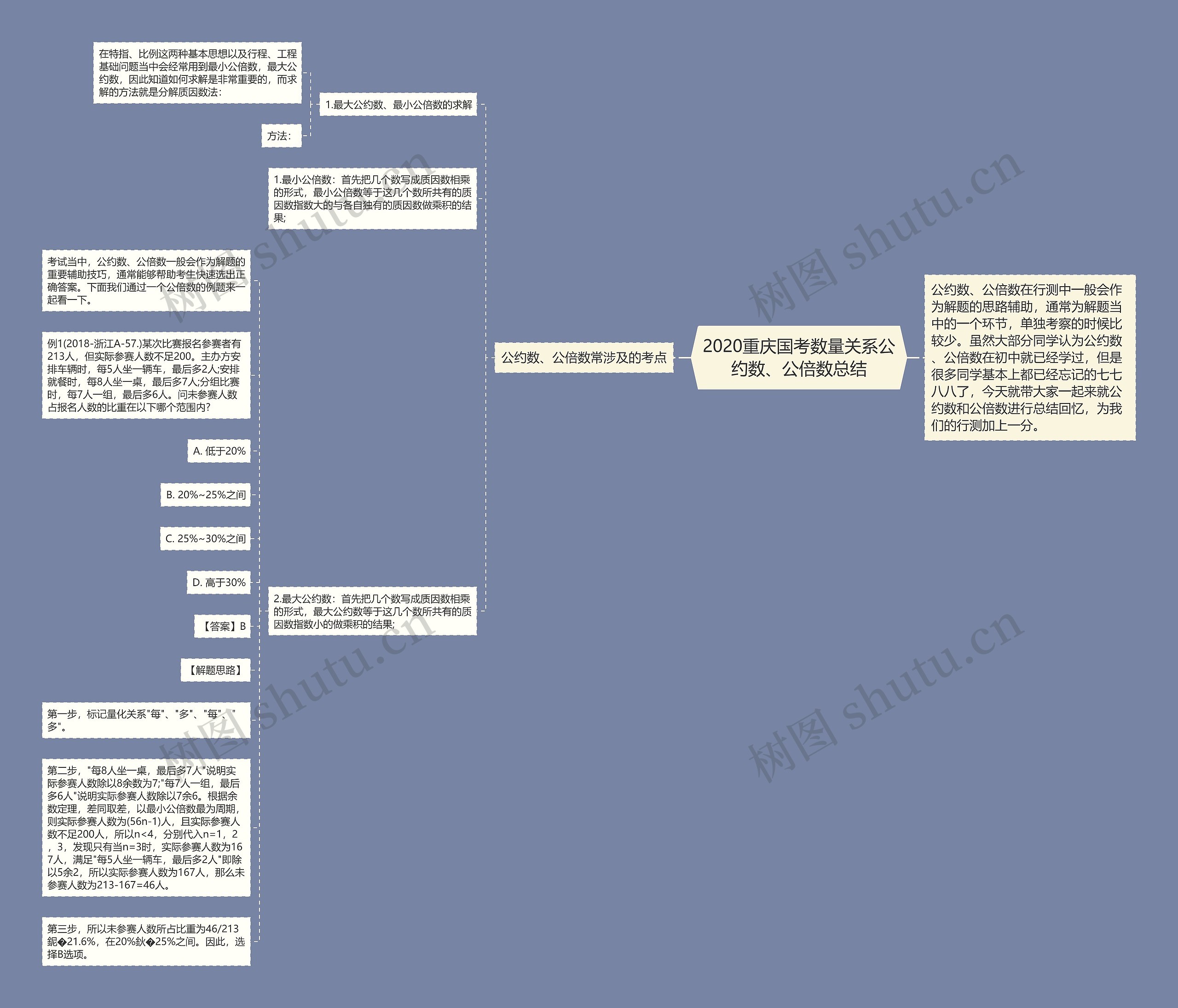
公约数、公倍数在行测中一般会作为解题的思路辅助,通常为解题当中的一个环节,单独考察的时候比较少。
树图思维导图提供《2020重庆国考数量关系公约数、公倍数总结》在线思维导图免费制作,点击“编辑”按钮,可对《2020重庆国考数量关系公约数、公倍数总结》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0d2624243600f64c3b814a6ef506547a

公约数、公倍数在行测中一般会作为解题的思路辅助,通常为解题当中的一个环节,单独考察的时候比较少。
树图思维导图提供《2020重庆国考数量关系公约数、公倍数总结》在线思维导图免费制作,点击“编辑”按钮,可对《2020重庆国考数量关系公约数、公倍数总结》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:0d2624243600f64c3b814a6ef506547a