2022国考行测备考干货之乘积式增长率巧解数量关系思维导图

眼眶很热

2023-03-04

浏览量: 2

2022国考行测备考

乘积式增长率巧解

数量关系

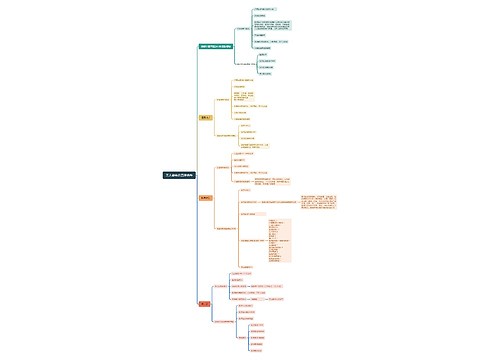
近年来，资料分析中增长率的考法愈加多变，乘积式增长率这种创新考法逐渐崭露头角，乘积式增长率指的是型如r=(现期量-基期量基期量)/基期量，求r的增长率，很多同学在实际做题的过程中对于求解此类增长率极为头疼，但如果理解透彻其原理，就迎刃而解.

树图思维导图提供《2022国考行测备考干货之乘积式增长率巧解数量关系》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测备考干货之乘积式增长率巧解数量关系》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：2e0676a3a6a833fcdd495ae7c4beb453

思维导图大纲

解法一：

第一步，本题考查经济利润问题，属于利润率折扣类，用赋值法解题。

第二步，根据盈利下降40%，赋值去年每吨利润为10，可得今年每吨盈利为10脳(1-40%)=6;根据销售量比去年增加了80%，赋值去年销售量为10，可得今年销售量为10脳(1+80%)=18，故去年总盈利为10脳10=100，今年总盈利为6脳18=108。

第三步，今年总盈利比去年增加

因此，选择B选项。

解法二：

第一步，本题考查经济利润问题，属于利润率折扣类。总盈利=每吨盈利脳销售量

第二步，由题目中三个量之间的关系，且最终求总盈利的增长率，可利用乘积式增长率思想即利用间隔增长率求解，由题目可知每吨盈利下降40%，销售量比去年增加了80%，得今年钢材的总盈利增长率为，即总盈利比去年增加了8%。

因此，选择B选项。

由解法二可以看出利用乘积式增长率思想能够直接用间隔增长率公式求解，更加方便快捷，可以达到巧解的目的，同学们可以跟着老师再做一个题巩固一下，学会熟练掌握此项巧解技能。

【例2】某网店连续3次下调某款手机的零售价格，每次下调幅度分别为：2.7%、5.5%和4.6%。经过3次调价，该款手机零售价较下调前大约下降了：

A.12.3% B. 12.8%

C.13.3% D.13.8%

【答案】A。华图解析：

解法一：

第一步，本题考查经济利润问题，属于基础公式类，用赋值法解题。

第二步，赋值原价为100元，根据"下调幅度分别为2.7%、5.5%和4.6%"，可得3次下调后价格为：100脳(1-2.7%)脳(1-5.5%)脳(1-4.6%)>100脳(1-2.7%-5.5%-4.6%)=100脳(1-12.8%)，故下降幅度小于12.8%，观察选项只有A满足。

因此，选择A选项。

解法二：

第一步，本题考查经济利润问题，属于基础公式类。

第二步，根据题目信息可以理解为第一次、第二次及第三次零售价格相对于下调前的增长率分别为：-2.7%、-5.5%、-4.6%，根据间隔增长率公式，利用两次间隔增长率求解可求出经过3次调价后零售价相对于下调前的增长率。100脳(1-2.7%)脳(1-5.5%)脳(1-4.6%)>100脳(1-2.7%-5.5%-4.6%)=100脳(1-12.8%)

第三步，，则，A选项最接近。

因此，选择A选项。

相信通过以上两个真题，同学们能够深入透彻理解乘积式增长率的求解思想，这在一定程度上能够简化计算的难度和减少计算的步骤，相信不管是在资料分析题目中还是数量关系题目中，同学们都能做到游刃有余巧解题目。

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图