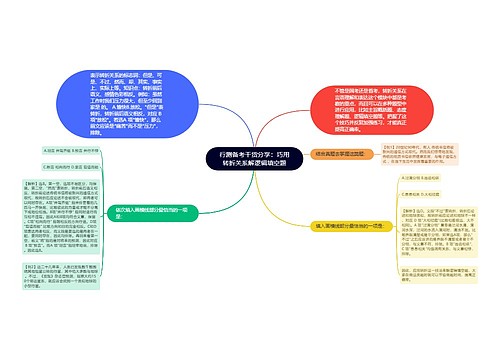
工程问题的备考干货：如何做到所向披靡思维导图

活在故事里

2023-03-04

浏览量: 1

工程问题

备考干货

很多同学都说，在备考行测的过程当中，数量关系一直是他们放弃的首选目标，时间少任务重，如果仅凭运气去蒙题准确性也不高，这也让部分考在笔试的时候没能够获取高分，面试也很难逆袭。那么如何学好数量关系呢。

树图思维导图提供《工程问题的备考干货：如何做到所向披靡》在线思维导图免费制作，点击“编辑”按钮，可对《工程问题的备考干货：如何做到所向披靡》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：682a4dcee651bdcf8c6c7f00758dd6dd

思维导图大纲

3.当工作总量一定时，工作时间与工作效率成反比

那今天我们来看一下工程问题当中的题型-给定时间型：题干中给出不同主语单独做工完成所需要的时间

赋值法给定时间型：

第一步：赋值工作总量是时间的最小公倍数;

第二步：求出效率=总量/时间;

第三步：利用总量相等，列等式，求时间。

例题讲解

【例】一项工程由甲、乙工程队单独完成，分别需50天和80天。若甲、乙工程队合作20天后，剩余工程量由乙、丙工程队合作需12天完成，则丙工程队单独完成此项工程所需的时间是：

A.40天

B.45天

C.50天

D.60天

【华图解析】

第一步，阅读题干，发现给了不同主语单独做工完成所需要的时间，因此考查工程问题的给定时间型。

第二步，赋值工作总量为50和80的最小公倍数400，则甲的工作效率为8，乙的工作效率为5。设丙的工作效率为X，根据题意可得总量=前20天量+后12天量，则为20脳(8+5)+12脳(5+X)=400，解得X=20/3，则丙单独完成所需的时间为总量梅效率=时间，则为400梅20/3=60(天)。

因此，选择D选项。

思路应用

【例】手工制作一批元宵节花灯，甲、乙、丙三位师傅单独做，分别需要40小时、48小时、60小时完成。如果三位师傅共同制作4小时后，剩余任务由乙、丙一起完成，则乙在整个花灯制作过程中所投入的时间是( )。

A. 24小时

B. 25小时

C. 26小时

D. 28小时

【答案】A

【华图解析】第一步，阅读题干，发现给了不同主语甲乙丙单独做工完成所需要的时间，因此考查工程问题的给定时间型。

第二步，赋值工作总量为 240，赋为40、48 和 60 的最小公倍数，则甲的效率为 6，乙的效率为 5，丙的效率为 4。甲、乙、丙三个师傅先共同制作 4 小时，可以完成的工作量为(6+5+4)脳4=60，剩余任务由乙、丙一起完成，需要的时间=剩余总量梅效率=(240-60)梅(5+4)=20小时，则乙投入的总时间为 4+20=24(小时)。答案选择 A。

通过上面的例题可以看出，工程问题的给定时间型题目，要对这种题目的判别了解，同时也要掌握这类题型的解题步骤。学会相应技巧之后，需要进行一定的题目练习以提高对技巧的熟练掌握度和增加自己的题目储备量。从而在以后的做题过程中，能够快速解决此类问题，从而在考试过程中取得相应的分数。

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图