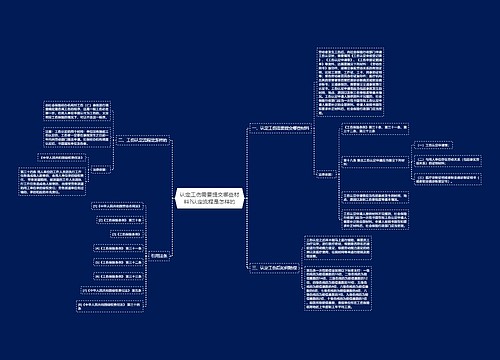
2022年国考行测数量关系中的“相遇”思维导图

堕落时代

2023-03-04

浏览量: 2

国家公务员考试行测备考

国考数量关系

2022年国考行测数量关系中的“相遇”详情见下文：

树图思维导图提供《2022年国考行测数量关系中的“相遇”》在线思维导图免费制作，点击“编辑”按钮，可对《2022年国考行测数量关系中的“相遇”》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：ac57d519bda6444a1ea3f36b5435ccad

思维导图大纲

直线相遇

直线相遇的题型特征是相距两地、同时出发、相向而行，三种特征同时具备时就可以判定本题属于相遇问题。识别题型后，接下来小编为大家讲解一下具体应该如何求解。

两人相距路程S,分别从两端同时出发，速度分别为v1和v2，经过时间t后两人相遇，则两人行驶的路程分别为v1t和v2t，相遇的总路程为S=v1t+v2t=(v1+v2)t，这就是直线相遇问题的公式。

【例】小华和小图，分别在A和B点同时出发，相向而行，二人速度分别为80米/分钟、100米/分钟，同时出发4分钟后相遇，则AB两地的距离是多少?

【解析】本题符合直线相遇问题的基本特征，速度、时间均具备，只需要代入公式即可求解。小华和小图相距A、B两地，同时出发，相向而行，故将数据代入公式S=(v1+v2)t，可得AB两地的距离SAB=(80+100)脳4=720米。

环形相遇

环形相遇的题型特征为环形跑道，通常是同点且同时出发，背向而行。

与直线相遇相似，环形一圈的距离为S，两人从同一地点同时出发，两人速度分别为v1和v2，经过时间t后两人相遇，则两人行驶的路程分别为v1t和v2t,则相遇的总路程为S=v1t+v2t=(v1+v2)t=一圈的距离，但是环形相遇可能会发生多次，即两人相遇N次，那么共行驶的总距离应该是N圈，公式变化为：NS=(v1+v2)t。

【例】小华和小图，从环形跑道的同一点同时出发，背向而行，二人速度分别为米70米/分钟、90米/分钟，3分钟后相遇，则跑道一圈的距离是多少?

【解析】本题符合环形相遇问题的基本特征，小华和小图在环形跑道同一点同时背向出发，速度与时间同时具备，只需将数据代入公式，即可得到跑道一圈的距离=(v1+v2)t=(70+90)脳3=480米。

下面小编带领大家做一道真题感知一下相遇问题在考试中是如何考查的!

【例】已知A、B两地相距600千米。甲、乙两车同时从A、B两地相向而行，3小时相遇。若甲的速度是乙的1.5倍，则甲的速度是多少?

A.80千米/小时 B.90千米/小时

C.100千米/小时 D.120千米/小时

【解析】甲、乙两车相距两地，同时出发，相向而行，本题考查直线相遇问题，已知总距离和相遇时间，设乙的速度为v，则甲的速度为1.5v。根据公式S总=(v1+v2)t，代入数据得600=(v+1.5v)脳3，解得v=80，故甲的速度为1.5脳80=120(千米/小时)。

因此，选择D选项。

通过小编的讲解，大家是不是对相遇问题有了清晰地把握呀，小编给大家做了思维导图，便于建立比较完善的知识点系统，各位小伙伴赶紧拿小本本记下来，同时，备考过程中一定要多做题，方能将这些知识点融会贯通、熟练掌握，小编相信大家一定会上岸的!

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图