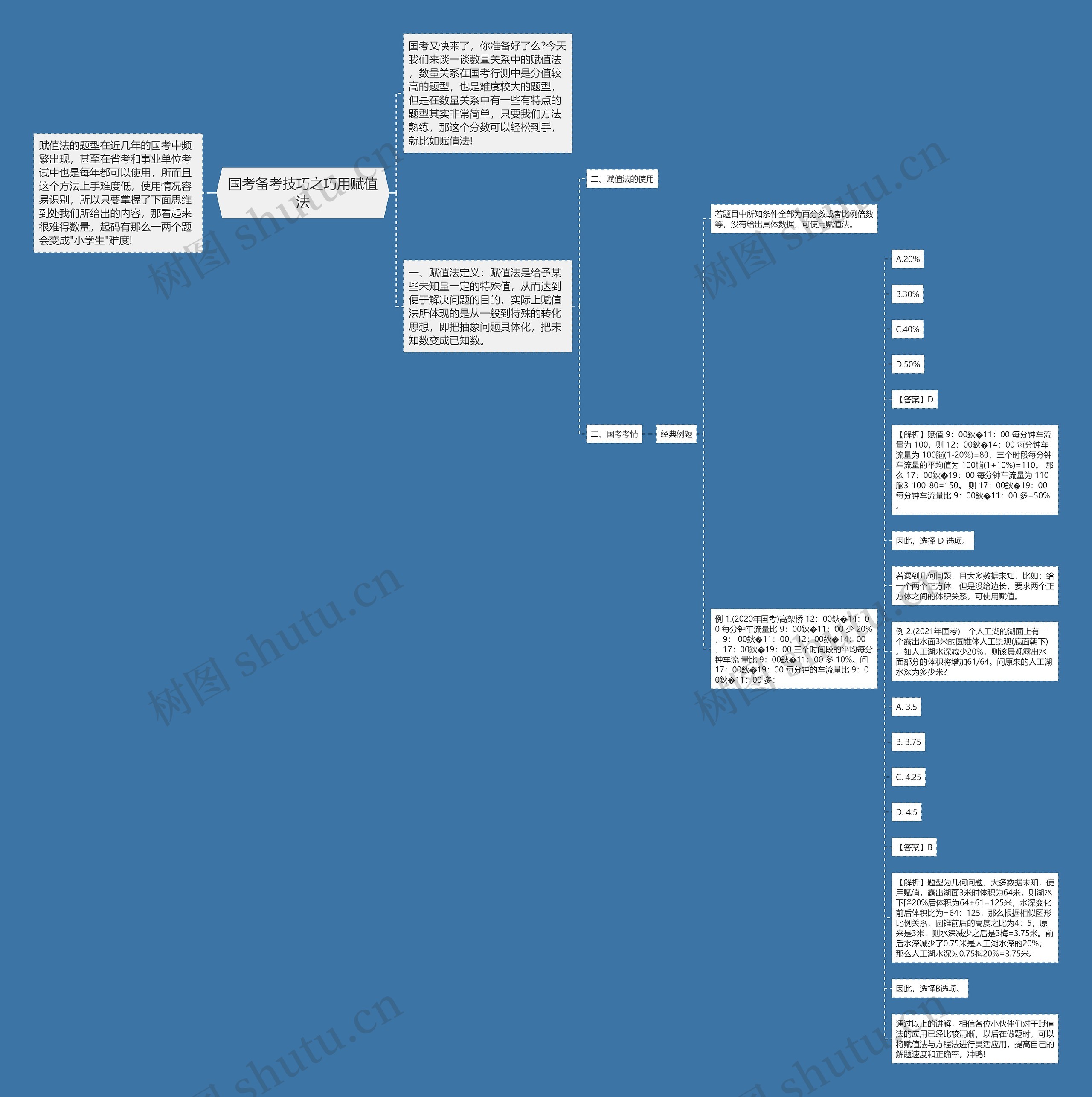
【解析】赋值 9:00鈥�11:00 每分钟车流量为 100,则 12:00鈥�14:00 每分钟车流量为 100脳(1-20%)=80,三个时段每分钟车流量的平均值为 100脳(1+10%)=110。 那么 17:00鈥�19:00 每分钟车流量为 110脳3-100-80=150。 则 17:00鈥�19:00 每分钟车流量比 9:00鈥�11:00 多=50%。
若遇到几何问题,且大多数据未知,比如:给一个两个正方体,但是没给边长,要求两个正方体之间的体积关系,可使用赋值。
例 2.(2021年国考)一个人工湖的湖面上有一个露出水面3米的圆锥体人工景观(底面朝下)。如人工湖水深减少20%,则该景观露出水面部分的体积将增加61/64。问原来的人工湖水深为多少米?
【解析】题型为几何问题,大多数据未知,使用赋值,露出湖面3米时体积为64米,则湖水下降20%后体积为64+61=125米,水深变化前后体积比为=64:125,那么根据相似图形比例关系,圆锥前后的高度之比为4:5,原来是3米,则水深减少之后是3梅=3.75米。前后水深减少了0.75米是人工湖水深的20%,那么人工湖水深为0.75梅20%=3.75米。
通过以上的讲解,相信各位小伙伴们对于赋值法的应用已经比较清晰,以后在做题时,可以将赋值法与方程法进行灵活应用,提高自己的解题速度和正确率。冲鸭!