国考行测数量关系知识点解题技巧思维导图
风雪夜人归
2023-03-03
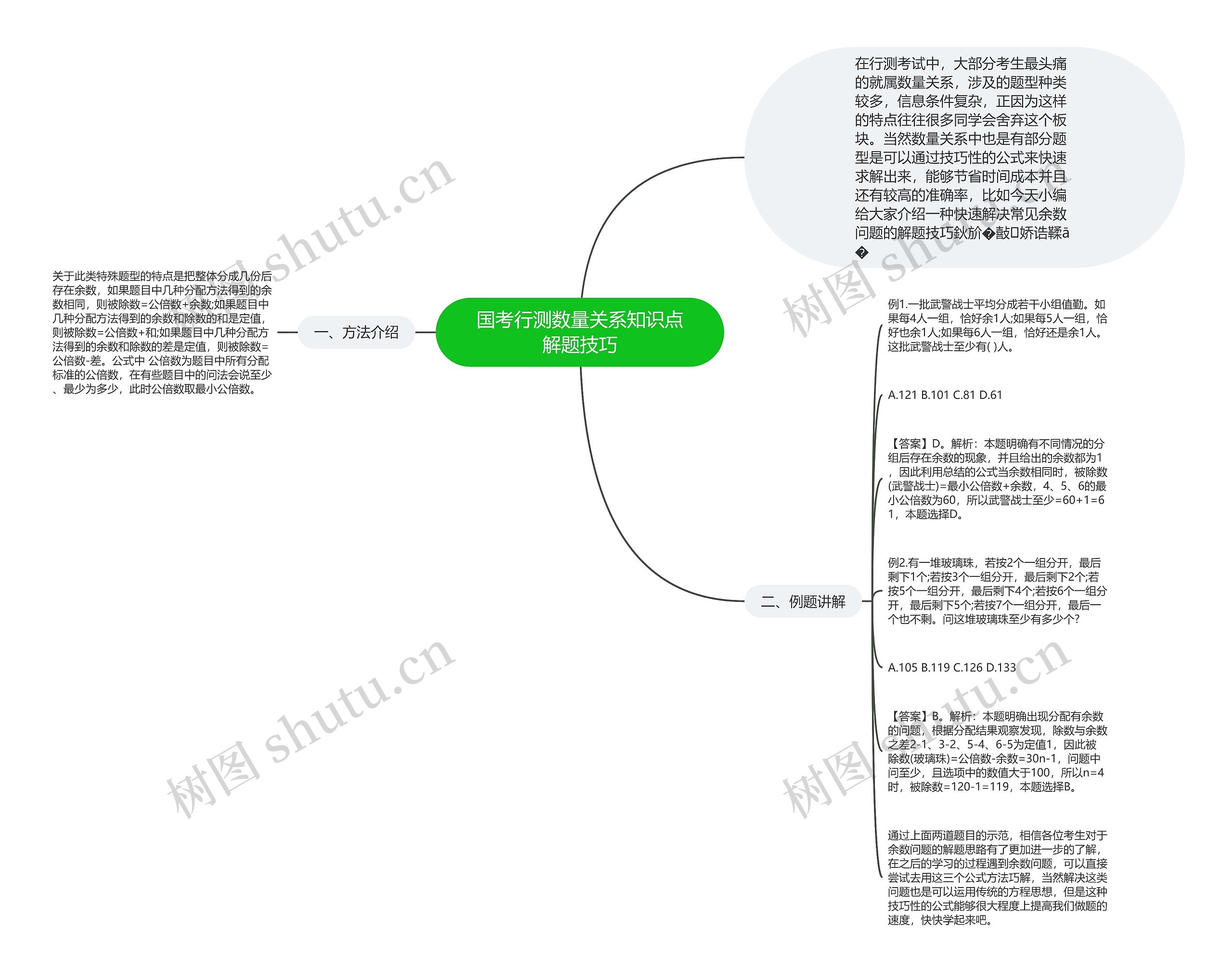
在行测考试中,大部分考生最头痛的就属数量关系,涉及的题型种类较多,信息条件复杂,正因为这样的特点往往很多同学会舍弃这个板块。
树图思维导图提供《国考行测数量关系知识点解题技巧》在线思维导图免费制作,点击“编辑”按钮,可对《国考行测数量关系知识点解题技巧》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:cb89244a905bf2b850050450faa78a7c
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
 U633687664
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作,点击“编辑”按钮,可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

抓住重点思维导图
 ~漫埗陽茪~
~漫埗陽茪~树图思维导图提供《抓住重点》在线思维导图免费制作,点击“编辑”按钮,可对《抓住重点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4c49e4799ddf94a339c56e46eb96a826

相似思维导图模版
思维导图模版推荐
海西州人民政府办公室关于成立海西州生产安全事故调查处理委员会的通知(海西州人民政府办公室发布)思维导图
2023-03-03 21:53:00

国考面试答题技巧——“乡村振兴”相关题目的答题思路思维导图
2023-03-03 21:53:03

2022国考行测言语理解:指哪打哪之细节查找题思维导图
2023-03-03 21:53:08

平顶山市教育局转发河南省教育厅关于加强中小学校师生集体外出活动安全管理的通知(平顶山市教育局发布)思维导图
2023-03-03 21:52:56
【公基备考】时政热点分析《中国共产党的历史使命和行动价值》其二思维导图
2023-03-03 21:52:55
公基法律之代位继承与转继承思维导图
2023-03-03 21:52:50