高层建筑抗震设计中短柱问题的处理、分析思维导图

孤败

2023-03-01

浏览量: 5

处理

分析

问题

设计

建筑

高层

截面

框架

提高

承载

工程纠纷

建筑工程管理

工程设计管理

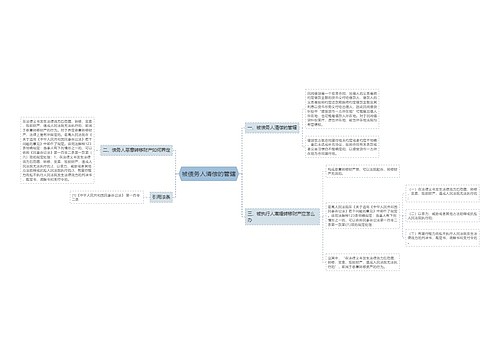
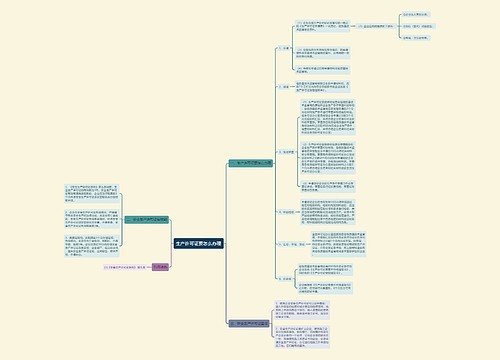
在层高一定的情况下，为提高延性而降低轴压比则会导致柱截面增大，且轴压比越小截面越大；而截面增大导致剪跨比减小，又降低了构件的延性。因此，在高层特别是超高层建筑结构设计中，为满足规程［1］对轴压比限值的要求，柱子的截面往往比较大，在结构底部常常形成短柱甚至超短柱。另外，诸如图书馆的书库、层高较低的储藏室、高层建筑的地下车库等由于使用荷载大，层高较低，在设计中也不可避免地会出现短柱。众所周知，短柱的延性很差，尤其是超短柱几乎没有延性，在建筑遭受本地区设防烈度或高于本地区设防烈度的地震影响时，很容易发生剪切破坏

树图思维导图提供《高层建筑抗震设计中短柱问题的处理、分析》在线思维导图免费制作，点击“编辑”按钮，可对《高层建筑抗震设计中短柱问题的处理、分析》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：5df0aa07d7f56cf6b0e56728b51fc423

思维导图大纲

1、短柱的正确判定

规程［1］和规范［2］都规定，柱净高H与截面高度h之比H／h≤4为短柱，工程界许多工程技术人员也都据此来判定短柱，这是一个值得注意的问题。因为确定是不是短柱的参数是柱的剪跨比λ，只有剪跨比λ＝M／Vh≤2的柱才是短柱，而柱净高与截面高度之比H／h≤4的柱其剪跨比λ不一定小于2，亦即不一定是短柱。按H／h≤4来判定的主要依据是：

①λ＝M／Vh≤2；

②考虑到框架柱反弯点大都靠近柱中点，取M＝0.5VH，则λ＝M／Vh＝0.5VH／Vh＝0.5H／h≤2，由此即得H／h≤4.但是，对于高层建筑，梁、柱线刚度比较小，特别是底部几层，由于受柱底嵌固的影响且梁对柱的约束弯矩较小，反弯点的高度会比柱高的一半高得多，甚至不出现反弯点，此时不宜按H／h≤4来判定短柱，而应按短柱的力学定义——剪跨比λ＝M／Vh≤2来判定才是正确的。

框架柱的反弯点不在柱中点时，柱子上、下端截面的弯矩值大小就不一样，即Mt≠Mb.因此，框架柱上、下端截面的剪跨比大小也是不一样的，即λt＝Mt／Vh≠λb＝Mb／Vh.此时，应采用哪一个截面的剪跨比来判断框架柱是不是属于短柱呢？笔者认为，应该采用框架柱上、下端截面中剪跨比的较大值，即取λ＝max（λt，λb）。其理由如下：框架柱的受力情况有如一根受有定值轴压力的连续梁，柱高Hn相当于连续梁的剪跨a，已有的试验研究结果表明［10］：对于剪跨a不变的连续梁，当截面上、下配置的纵筋相同时，剪切破坏总是发生在弯矩较大的区段；对于框架柱，临界斜裂缝也总是发生在弯矩较大的区段。

事实上，在柱高Hn或连续梁剪跨a的范围内，最大剪跨比是出现在弯矩较大区段上的。钢筋砼构件的抗剪承载力是随剪跨比λ增大而降低的。所以，同样条件下，弯矩较大区段的截面抗剪承载力要比弯矩较小区段的小，在荷载作用下，如果发生剪切破坏，就只能是在弯矩较大区段上。用来判断框架柱是否属于短柱的剪跨比λ当然应是可能发生剪切破坏截面的剪跨比λ。

一般情况下，在高层建筑的底部几层，框架柱的反弯点都偏上，即Mb＞Mt.此时，可按式（1）或式（2）判定短柱：

或Hn／h≤2／yn（2）

式中，yn- -n层柱的反弯点高度比，根据几何关系，可得：yn＝1／（1＋Ψ），其中，Ψ＝Mt／Mb，0≤Ψ≤1；

Hn- -n层柱的净高。

式（2）具有一般性。当反弯点在柱中点时，Ψ＝1，yn＝0.5，式（2）即成为Hn／h≤4；当反弯点在柱上端截面时，Ψ＝0，yn＝1，式（2）即成为Hn／h≤2；如果框架柱上不出现反弯点，就应采用最大弯矩作用截面的剪跨比λ＝M／Vh≤2来判断短柱。?

2、改善短柱抗震性能的措施

当按剪跨比λ判定柱子不是短柱时，按一般框架柱的抗震要求采取构造措施即可；确定为短柱后，就应当尽量提高短柱的承载力，减小短柱的截面尺寸，采取各种有效措施提高短柱的延性，改善短柱的抗震性能。

2.1 使用复合螺旋箍筋

高层建筑框架柱的抗剪能力是应该满足剪压比限值和“强剪弱弯”要求的，柱端的抗弯承载力也是应该满足“强柱弱梁”要求的。对于短柱，只要符合“强剪弱弯”和“强柱弱梁”的要求，是能够做到使其不发生剪切型破坏的。因此，使用复合螺旋箍筋［4］来提高柱子的抗剪承载力，改善对砼的约束作用，能够达到改善短柱抗震性能的目的。

2.2 采用分体柱

由于短柱的抗弯承载力比抗剪承载力要大得多，在地震作用下往往是因剪坏而失效，其抗弯强度不能完全发挥。因此，可人为地削弱短柱的抗弯强度，使抗弯强度相应于或略低于抗剪强度，这样，在地震作用下，柱子将首先达到抗弯强度，从而呈现出延性的破坏状态。

人为削弱抗弯强度的方法，可以在柱中沿竖向设缝将短柱分为2或4个柱肢组成的分体柱，分体柱的各柱肢分开配筋。在组成分体柱的柱肢之间可以设置一些连接键，以增强它的初期刚度和后期耗能能力。一般，连接键有通缝、预制分隔板、预应力摩擦阻尼器、素砼连接键等形式。

对分体柱工作性态的理论分析和试验研究表明［3～4］：采用分体柱的方法虽然使柱子的抗剪承载力基本不变，抗弯承载力稍有降低，但是使柱子的变形能力和延性均得到显著提高，其破坏形态由剪切型转化为弯曲型，从而实现了短柱变“长柱”的设想，有效地改善了短柱尤其是剪跨比λ≤1.5的超短柱的抗震性能。分体柱方法已在实际工程中得到应用［5］。

2.3 采用钢骨砼柱

钢骨砼柱由钢骨和外包砼组成。钢骨通常采用由钢板焊接拼制或直接扎制而成的工字形、口字形、十字形截面。

与钢结构相比，钢骨砼柱的外包砼可以防止钢构件的局部屈曲，提高柱的整体刚度，显著改善钢构件出平面扭转屈曲性能，使钢材的强度得以充分发挥。采用钢骨砼结构，一般可比钢结构节约钢材达50％以上［6］。

此外，外包砼增加了结构的耐久性和耐火性。与钢筋砼结构相比，由于配置了钢骨，使柱子的承载力大大提高，从而有效地减小柱截面尺寸；钢骨翼缘与箍筋对砼有很好的约束作用，砼的延性得到提高，加上钢骨本身良好的塑性，使柱子具有良好的延性及耗能能力。

由于钢骨砼柱充分发挥了钢与砼两种材料的特点，具有截面尺寸小，自重轻，延性好以及优越的技术经济指标等特点，如果在高层或超高层钢筋砼结构下部的若干层采用钢骨砼柱，可以大大减小柱的截面尺寸，显著改善结构的抗震性能。

2.4 采用钢管砼柱钢管砼是由砼填入薄壁圆形钢管内而形成的组合结构材料，是套箍砼的一种特殊形式。由于钢管内的砼受到钢管的侧向约束，使得砼处于三向受压状态，从而使砼的抗压强度和极限压应变得到很大的提高，砼特别是高强砼的延性得到显著改善。同时，钢管既是纵筋，又是横向箍筋，其管径与管壁厚度的比值至少都在90以下，这相当于配筋率至少都在4.6％以上，这远远超过抗震规范［2］对钢筋砼柱所要求的最小配筋率限值。由于钢管砼的抗压强度和变形能力特佳，即使在高轴压比条件下，仍可形成在受压区发展塑性变形的“压铰”，不存在受压区先破坏的问题，也不存在像钢柱那样的受压翼缘屈曲失稳的问题。因此，从保证控制截面的转动能力而言，无需限定轴压比限值［8］。规程［9］规定，钢管砼单肢柱的承载力可按式（3）计算：N≤φ1φeN0（3）

式中，；

φ1，φe的物理意义及计算方法见规程［9］。

由式（3）可以看出，当选用了高强砼和合适的套箍指标θ后，柱子的承载力可大幅度提高，通常柱截面可比普通钢筋砼柱减小一半以上，消除了短柱并具有良好的抗震性能。

3、小结

1、确定是不是短柱不宜按H／h≤4来判别，而应按剪跨比λ＝M／Vh≤2来判别。一般情况下，可采用本文式（2）来判别。当需要初步判别是否属于短柱时，可先按D值法确定反弯点高度比yn，然后按本文式（2）来判别。

2、当按剪跨比λ判定柱子不是短柱时，按一般框架柱的抗震要求采取构造措施即可；确为短柱，就应当尽量提高短柱的承载力，减小短柱的截面尺寸，采取各种有效措施提高短柱的延性，改善短柱的抗震性能。使用复合螺旋箍筋，采用分体柱技术均可有效地改善短柱的抗震性能；采用钢骨砼、钢管砼等新结构，可显著提高柱的承载力，减小柱截面尺寸，避免在结构下部出现短柱尤其是超短柱。因此，在高层建筑抗震设计中应根据工程的具体情况，尽量采用上述新结构、新技术，来避免短柱脆性破坏问题的发生！

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图