高一下学期数学期末知识点归纳思维导图
心不动则不痛
2022-12-21
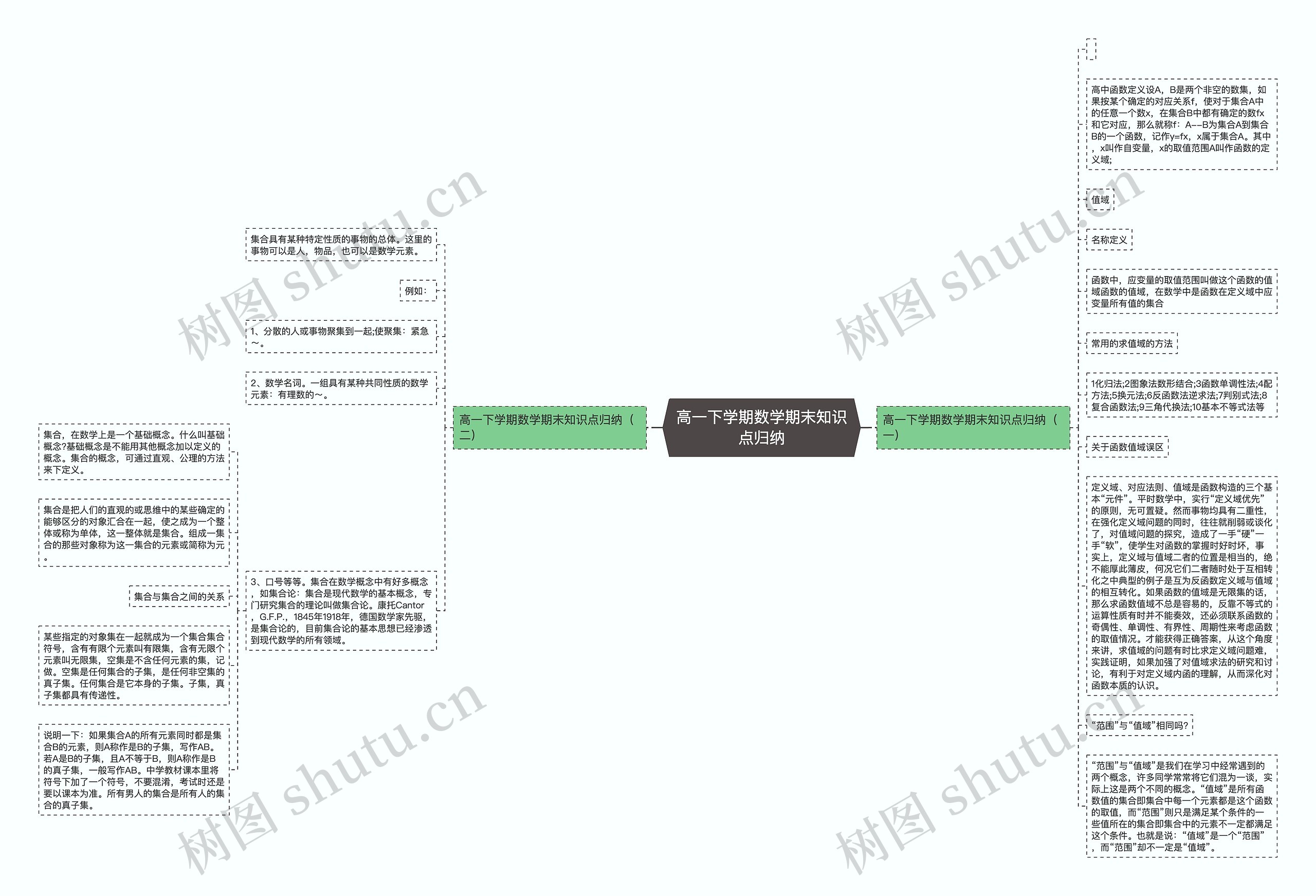
高一下学期数学期末的内容,包含了函数的定义、值域的求解方法、误区和范围和值域的区别,同时还包含了集合的概念和集合论。函数的定义包含了自变量、函数名、对应法则、定义域和值域,值域的求解方法包含了化归法、图象法数形结合、函数单调性法,同时还有许多需要注意的误区,集合作为一个重要的数学元素,在数学中也是一个重要的概念,我们可以更加深入地理解各种数学概念。
思维导图大纲
相关思维导图模版
高一数学教师下学期工作总结2023思维导图
 青衣衫
青衣衫树图思维导图提供《高一数学教师下学期工作总结2023》在线思维导图免费制作,点击“编辑”按钮,可对《高一数学教师下学期工作总结2023》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:01f005f91d91e5a2b58278b581fd25e1
高三数学期末教学总结思维导图
 失落感
失落感树图思维导图提供《高三数学期末教学总结》在线思维导图免费制作,点击“编辑”按钮,可对《高三数学期末教学总结》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:036029061636d7d76c7fcda78738f235