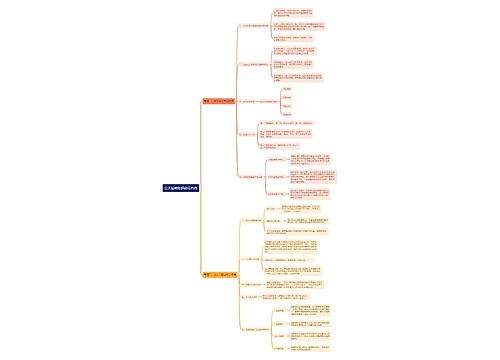
考研数学基础知识点梳理(高数篇)思维导图

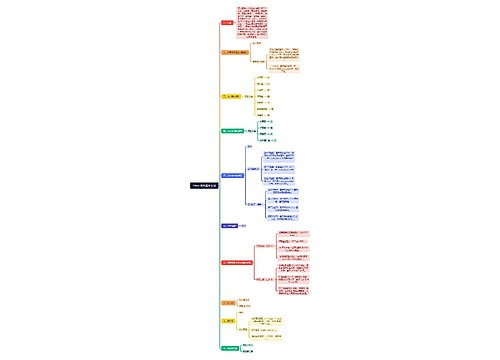
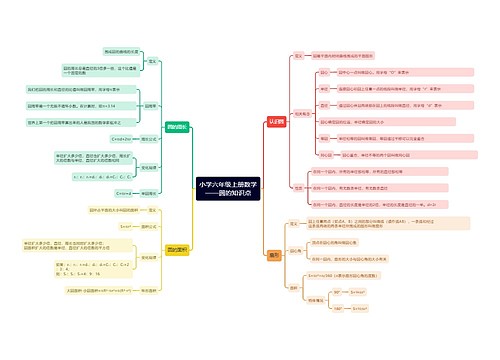
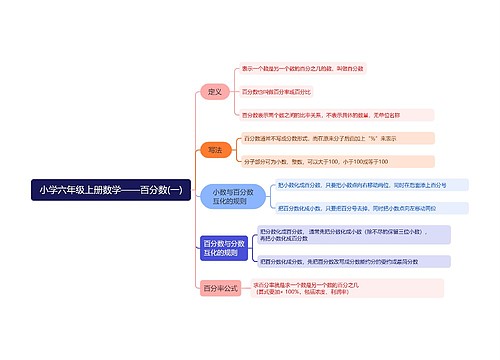
考研数学基础知识点梳理(高数篇)思维导图总共包含九章内容，第一章讲述了函数、极限与连续，介绍了函数的有界性、极限的定义及性质，极限的计算方法和函数的连续性，间断点的类型，和渐近线的计算。第二章则是导数与微分，重点总结了导数及微分的定义和计算方法，和导数的应用，第三章是中值定理，总结了闭区间上连续函数的性质、微分中值定理、积分中值定理、泰勒中值定理和费马引理。第四章讲述了一元函数积分学，包含原函数与不定积分的定义，不定积分的计算方法、定积分的定义、定积分性质、定积分的计算方法、定积分的应用，变限积分与广义积分，第五章是空间解析几何，重点讲述了向量的运算、直线与平面的方程关系和各种曲面方程的求法。第六章是多元函数微分学，重点介绍了二重极限和二元函数连续、偏导数、可微及全微分的定义，和二元函数偏导数存在、可微、偏导函数连续之间的关系、多元函数偏导数的计算方法、方向导数与梯度、多元函数的极值和空间曲线的切线与法平面、曲面的切平面与法线。第七章是多元函数积分学，除二重积分外，还包含第一、二类曲线积分及第一、二类曲面积分的计算及对称性、格林公式、高斯公式、斯托克斯公式和场论初步，第八章是微分方程，讲解了各类微分方程的求解、线性微分方程解的性质和应用。最后一章则讲述了级数，包含收敛级数的性质、正项级数的判别法、交错级数的莱布尼兹判别法、绝对收敛与条件收敛、幂级数的收敛半径与收敛域、幂级数的求和与展开和傅里叶级数。