1. 给我最大的幸福不是知识,而是不断学习;不是现有的东西,而是不断获得;不是已经达到的高度,而是继续攀登。高斯
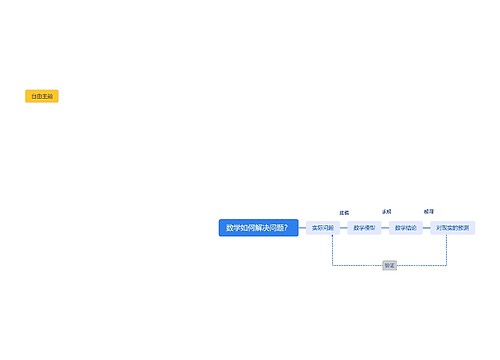
2. 在数学的领域中,提出问题的艺术比解答问题的艺术更为重要。
4. 只要一门科学分支能提出大量的问题,它就充满着生命力,而问题缺乏则预示着独立发展的终止或衰亡。
5. 一个人就好像一个分数,他的实际才能好比分子,而他对自己的估价好比分母。分母越大,则分数的值就越小。
6. 观察可能导致发现,观察将揭示某种规则、模式或定律。
7. 数学中的一些美丽定理具有这样的特点:它们很容易从事实中总结出来,但它们被证明是非常隐藏的。高斯
10. 新的数学方法和概念,常常比解决数学问题本身更重要。
11. 在数学中最令我欣喜的,是那些能够被证明的东西。
13. 无论数学的任何分支有多抽象,总有一天会应用到这个现实世界中。罗巴切夫斯基
14. 在数学中,我们发现真理的主要工具是归纳和模拟。
17. 尺有所短;寸有所长。物有所不足;智有所不明。
21. 一个有科学创新能力的人不但要有科学知识,还要有文化艺术修养。
22. 在现实中,没有像数学这样的东西,几千年依然如此美好。苏利文
23. 用心智的全部力量,来选择我们应遵循的道路。
25. 但数学享有盛誉的另一个原因是,数学给了各种精密自然科学一定程度的可靠性。没有数学,他们就无法获得这样的可靠性。――艾伯特爱因斯坦
26. 在现实中,不存在像数学那样有如此多的东西,持续了几千年依然是确实的如此美好。
27. 整数的简单构成,若干世纪以来一直是使数学获得新生的源泉。
28. 如果谁不知道正方形的对角线同边是不可通约的量,那他就不值得人的称号。
29. 无限!再也没有其他问题如此深刻地打动过人类的心灵。
31. 宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日常生活之谜,数学无处不在。华罗庚
32. 我总是尽我的精力和才能来摆脱那种繁重而单调的计算。
34. 数论是人类知识最古老的一个分支,然而他的一些最深奥的秘密与其最平凡的真理是密切相连的。
36. 数学比其他所有科学都更受尊重,因为它的命题是绝对可靠和无可争辩的,而其他科学往往有被新发现的事实推翻的危险。爱因斯坦
38. 数学主要的目标是公众的利益和自然现象的解释。
40. "如果谁不知道正方形的对角线同边是不可通约的量,那他就不值得人的称号。
44. 石可破也,而不可夺坚;丹可磨也,而不可夺赤。
46. 一个数学家的目的,是要了解数学。历史上数学的进展不外两途:增加对于已知材料的了解,和推广范围。
47. 尺有所短;寸有所长。物有所不足;智有所不明。
48. 数学家本质上是一个粉丝。如果他们不着迷,就没有数学。努瓦列斯
50. 数学无与伦比的永久性和万能性以及他对时间和文化背景的独立性是其本质的直接后果。埃博
51. 一个人的贡献和他的自负严格地成反比,这似乎是品行上的一个公理。
54. 一个没有几分诗人气的数学家永远成不了一个完全的数学家。
55. 门科学,只有成功运用数学,才能真正完善。马克思
57. 纯数学可以实用有用,应用数学也可以优美优雅。哈尔莫斯
61. 如果我继承可观的财产,我在数学上可能没有多少价值了。
63. 发现每一个新的群体在形式上都是数学的,因为我们不可能有其他的指导。
67. 石可破也,而不可夺坚;丹可磨也,而不可夺赤。
68. 不管数学的任一分支是多么抽象,总有一天会应用在这实际世界上。
69. 坚持不懈,烂木不折;坚持不懈,金石可以雕刻
70. 数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深。
71. 如果我们想要预见数学的将来,适当的途径是研究这门学科的历史和现状。
74. 可以数是属统治着整个量的世界,而算数的四则运算则可以看作是数学家的全部装备。
75. 给我五个系数,我讲画出一头大象;给我六个系数,大象将会摇动尾巴。
77. 纯数学这门科学再其现代发展阶段,可以说是人类精神之最具独创性的创造。
78. 青,取之于蓝而青于蓝;冰,水为之而寒于水。
81. 思维的运动形式通常是这样的:有意识的研究-潜意识的活动-有意识的研究。