数列思维导图
大灰
2023-04-25
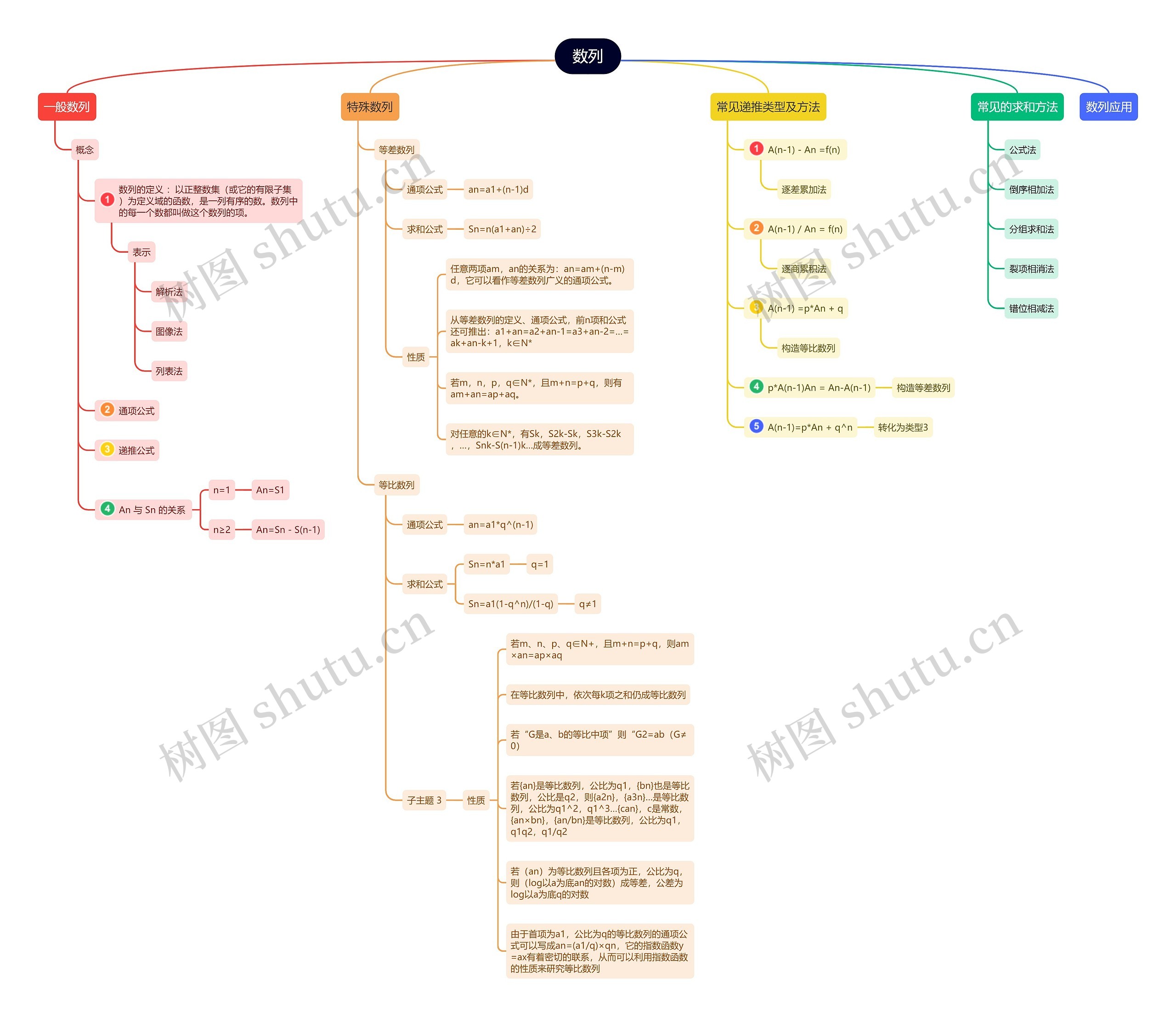
本图概括的是数列的概念、类型、特殊数列的通项公式和求和公式以及常用的求和方法。
树图思维导图提供《数列》在线思维导图免费制作,点击“编辑”按钮,可对《数列》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ed730bad2897c11eb02a8ad02ec1d855

本图概括的是数列的概念、类型、特殊数列的通项公式和求和公式以及常用的求和方法。
树图思维导图提供《数列》在线思维导图免费制作,点击“编辑”按钮,可对《数列》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:ed730bad2897c11eb02a8ad02ec1d855