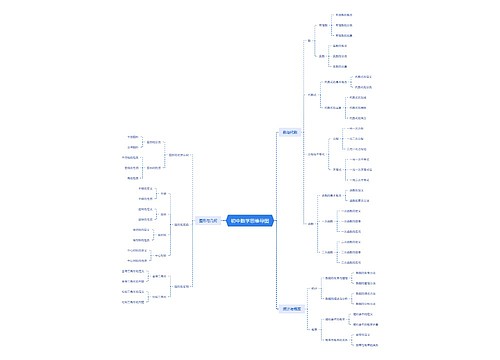
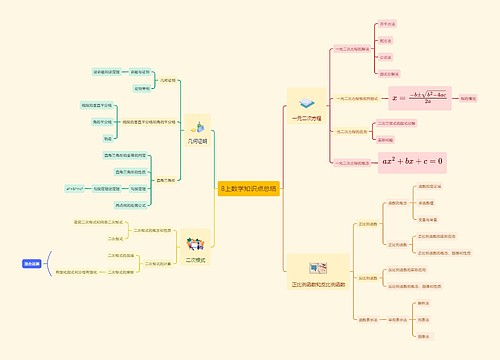
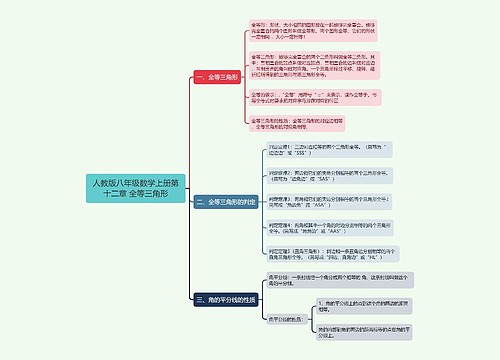
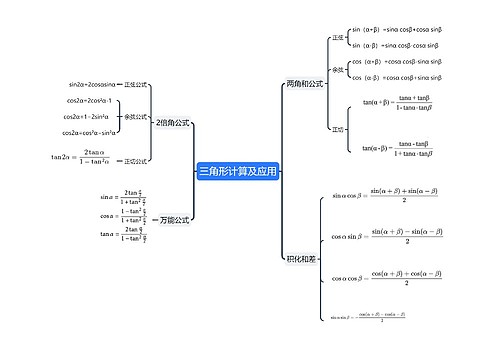
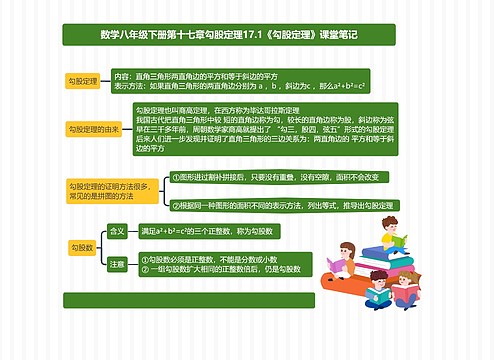
数学八年级下册第十七章勾股定理17.2《勾股定理的逆定理》课堂笔记思维导图
小王!
2023-04-21

这篇思维导图介绍了数学八年级下册第十七章勾股定理17.2《勾股定理的逆定理》课堂笔记
树图思维导图提供《数学八年级下册第十七章勾股定理17.2《勾股定理的逆定理》课堂笔记》在线思维导图免费制作,点击“编辑”按钮,可对《数学八年级下册第十七章勾股定理17.2《勾股定理的逆定理》课堂笔记》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:9e18856f524d6c634e4fce399c69e2a2
思维导图大纲
相关思维导图模版
数学八年级下册第十九章一次函数《课题学习 选择方案》课堂笔记思维导图
树图思维导图提供《数学八年级下册第十九章一次函数《课题学习 选择方案》课堂笔记》在线思维导图免费制作,点击“编辑”按钮,可对《数学八年级下册第十九章一次函数《课题学习 选择方案》课堂笔记》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4912d4e84860e8d7289ab1fc46460698

数学八年级下册第二十章《课题学习 体质健康测试中的数据分析》课堂笔记思维导图
树图思维导图提供《数学八年级下册第二十章《课题学习 体质健康测试中的数据分析》课堂笔记》在线思维导图免费制作,点击“编辑”按钮,可对《数学八年级下册第二十章《课题学习 体质健康测试中的数据分析》课堂笔记》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:c86fc20844878036783bece1b80b3131