小学数学圆柱的体积教学设计思维导图

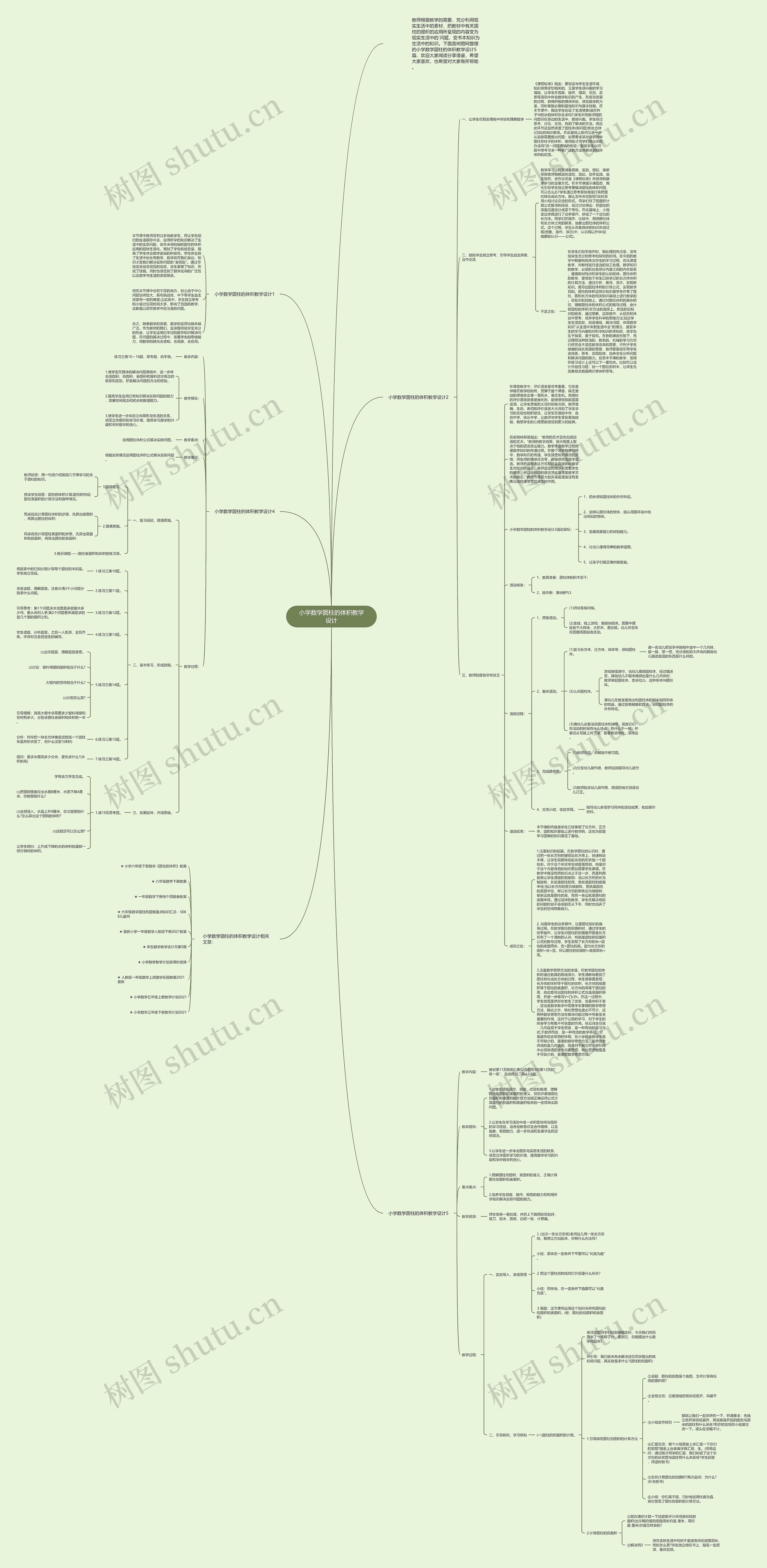
关于小学数学圆柱的体积教学设计思维导图，教师应该根据教学需要，利用现实生活中的素材，把教材中的知识变为生活中的知识。在教学设计中，让学生回归到生活原形中去，应用所学的知识解决了生活中的实际问题，增加了学生的信息量，提高了学生的学习兴趣和积极性，同时也感受到了数学与生活的紧密联系。在教学中，要让学生现实情境中体验和理解数学，创设与学生生活环境、知识背景密切相关的、又是学生感兴趣的学习情境，同时鼓励学生独立思考，引导学生自主探索、合作交流，这样可以让学生掌握知识、形成技能，并从问题中思考寻求一种更广泛的方法来解决原本枯燥的数学知识。