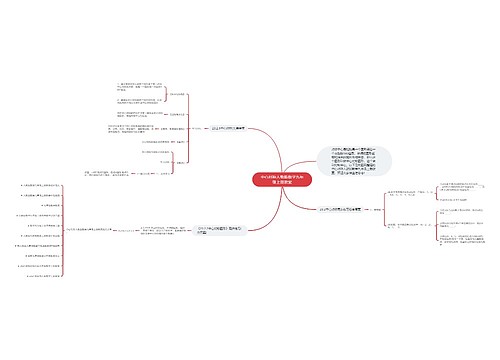
图形的旋转人教版数学九年级上册教案思维导图
最美的情书
2023-04-04

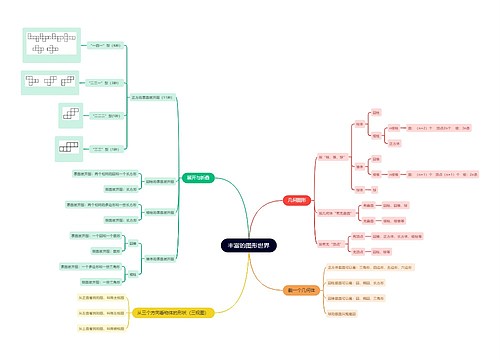
图形的旋转的相关知识点,旋转是指在平面内,将一个图形绕一点按某个方向旋转一定角度的运动,这个点叫做旋转中心,转动的角叫做旋转角,对应点的概念和应用、旋转的基本性质和图形旋转的特征。学生需要通过练习,学会如何画一个图形关于一条直线(对称轴)的对称图形,并了解什么是轴对称图形,也通过转动的钟表和风车,引导学生理解旋转,模板概括一些测试和练习,让学生检验自己是否掌握了相关知识点。
思维导图大纲
相关思维导图模版
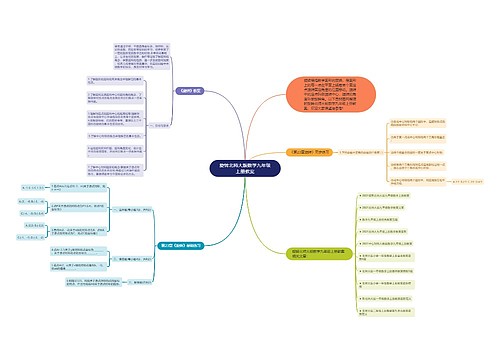
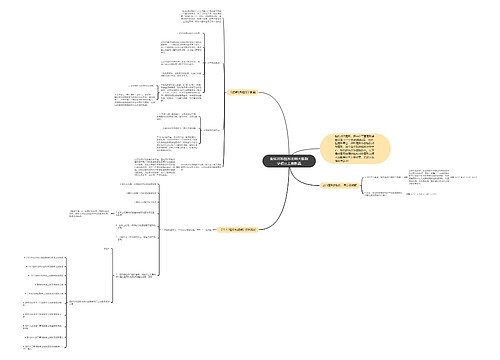
图案设计人教版数学九年级上册教案思维导图
 泪尽
泪尽树图思维导图提供《图案设计人教版数学九年级上册教案》在线思维导图免费制作,点击“编辑”按钮,可对《图案设计人教版数学九年级上册教案》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:4e620cc0b2061c47d68f1f32da153907
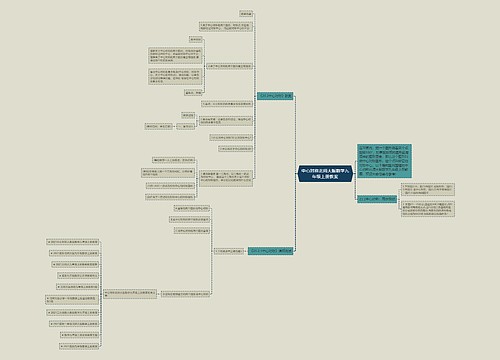
中心对称人教版数学九年级上册教案思维导图
 心奴
心奴树图思维导图提供《中心对称人教版数学九年级上册教案》在线思维导图免费制作,点击“编辑”按钮,可对《中心对称人教版数学九年级上册教案》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:91fee62802931d30c2268e40731f08e6