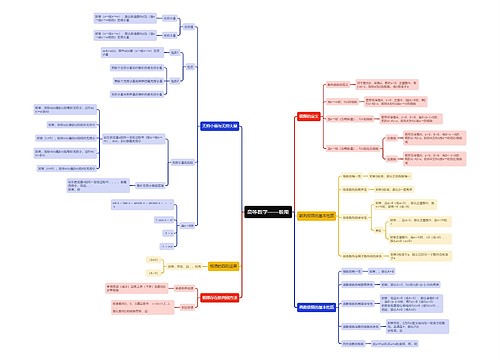
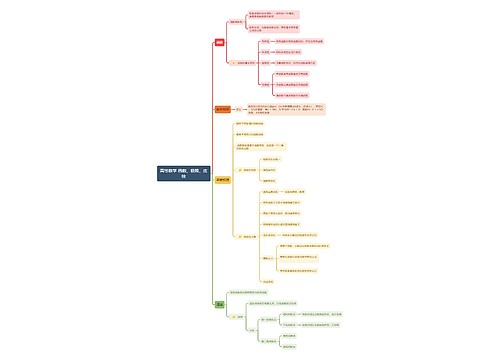
《高等数学》微分学思维导图
ZYJ
2022-11-15
《高等数学》微分学思维导图是微积分中的知识点,微积分中的可微、可导与连续都需要满足特定的条件,而可微即可导,可导推连续,左导数存在则左连续,右导数存在则右连续,多元微分中,可微则可偏导,连续,可偏导与连续互不相关,且皆无法推出可微,偏导数连续则可微,有可微的判定式。微积分中求导有按定义求导和求导公式两种方法,且有链式求导法和一阶微分形式不变性。导数的应用有研究函数的性态、费马定理、极值与最值、微分中值定理、拉格朗日中值定理、罗尔定理、柯西中值定理、泰勒公式,导数的几何应用有切线、法线、截距和微分中值定理。微积分中还有构造原函数、证明微分等式、不等式、一元函数的拐点、渐近线等内容。利用单调性求极值、找等值点、求区间内最值问题可以转化为方程和不等式的求解,一些特定的问题可以使用Taylor展开及Lagrange中值定理、不定中值不等式、凹凸性不等式。