大学物理-电磁场知识点思维导图
U77418911
2022-10-04
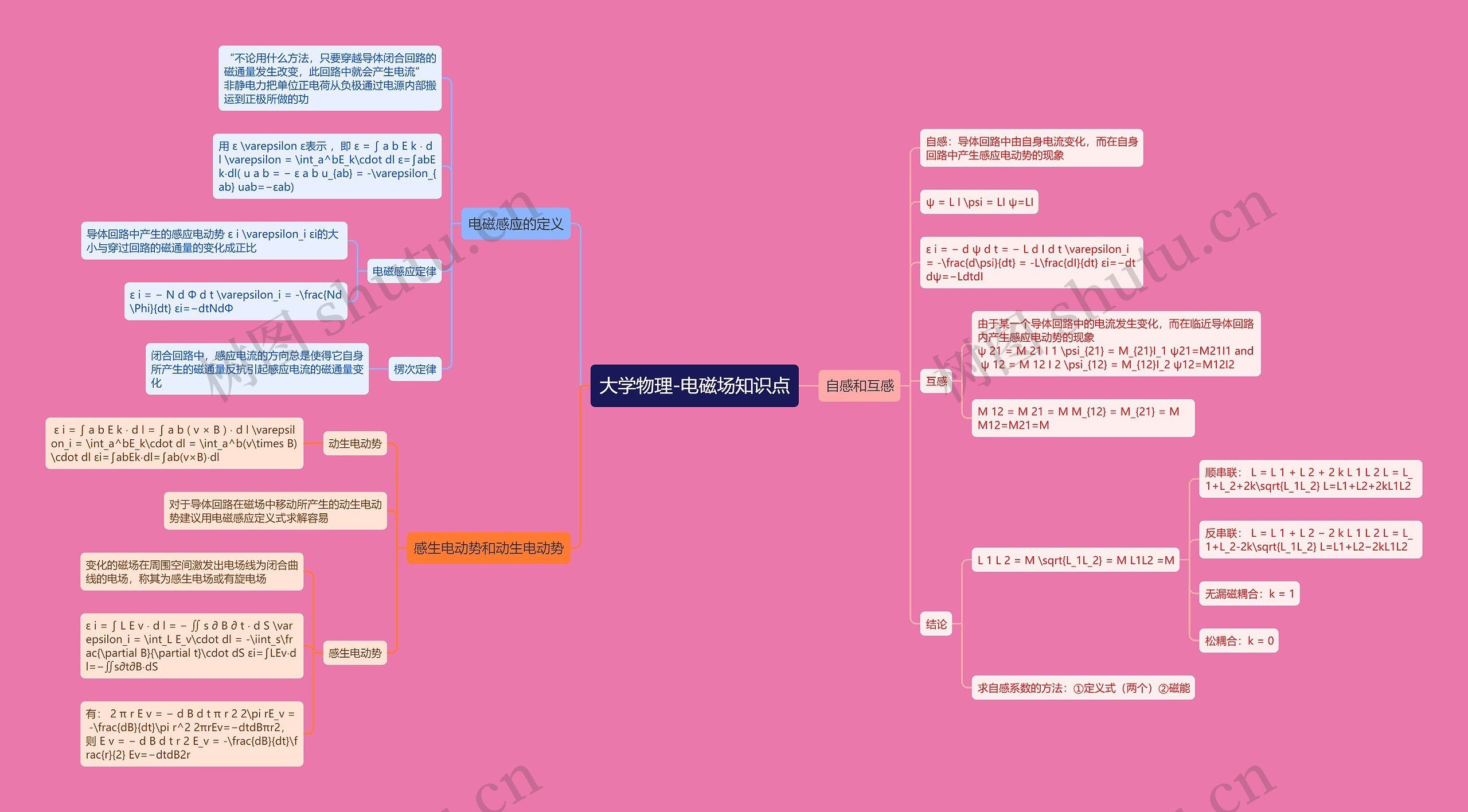
大学物理-电磁场知识点,电磁感应的定义、感生电动势和动生电动势、自感和互感
树图思维导图提供《大学物理-电磁场知识点》在线思维导图免费制作,点击“编辑”按钮,可对《大学物理-电磁场知识点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:685300c72031dbfda57bedaf6edba126

大学物理-电磁场知识点,电磁感应的定义、感生电动势和动生电动势、自感和互感
树图思维导图提供《大学物理-电磁场知识点》在线思维导图免费制作,点击“编辑”按钮,可对《大学物理-电磁场知识点》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:685300c72031dbfda57bedaf6edba126