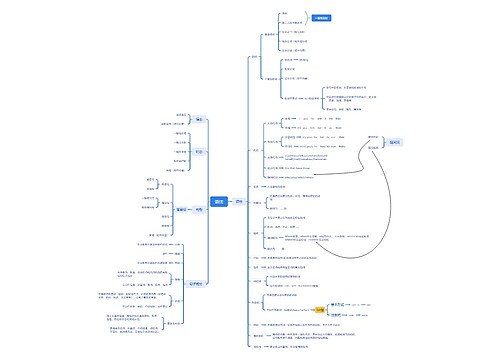
6. 导数和微分思维导图
U768868580
2024-08-18

导数微分,函数连续性,求导法则等内容讲解
树图思维导图提供《6. 导数和微分》在线思维导图免费制作,点击“编辑”按钮,可对《6. 导数和微分》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:3b8bbdc96fda50237d0a50e3d40b8993
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
 U633687664
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作,点击“编辑”按钮,可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

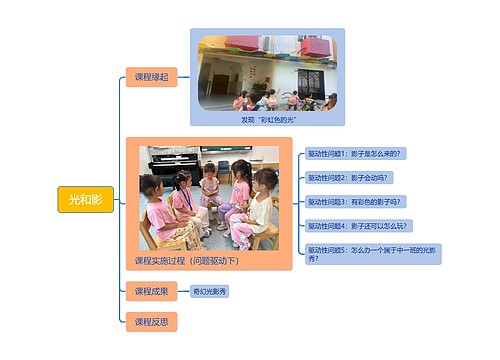
光和影思维导图
 小包卡麻麻
小包卡麻麻树图思维导图提供《光和影》在线思维导图免费制作,点击“编辑”按钮,可对《光和影》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:2f4c9606f70a3f8d98ec4d65695dc3d1