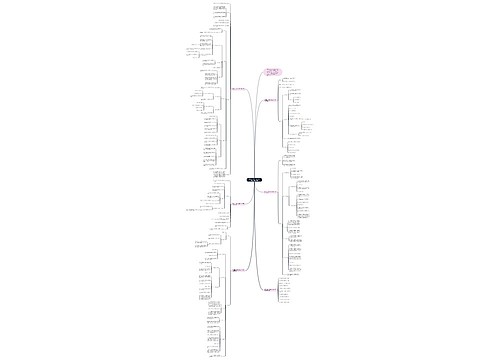
真题3:给出基本不等式的一种几何解释,并说明几何解释对数学学习的作用.
几何解释:一个圆的直径大于等于垂直该直径的弦。设该弦分该直径为两段,则该弦长为。可以利用射影定理或者相交弦定理容易求得。几何解释对数学学习的作用:几何中圆的垂径定理的知识解释均值不等式,借助形的几何直观性来阐明解释均值不等式,可称之为“以形助数”充分体现了数形结合的思想。这种利用“形”作为直观工具帮助学生理解和掌握知识、解决问题,使学生体会代数与几何之间的联系。
真题4:数学的产生与发展过程中蕴含着丰富的数学文化以“导数及其应用”教学为例,说明再数学教学中如何渗透数学文化;阐述数学文化对学生数学学习的作用。
(1)①数学史知识的渗透学生在学习高中数学导数知识的时候,由于是一个全新的概念,不同于在小学就有所接触的方程等知识。因此,学生对于导数的历史比较感兴趣,教师可以利用这一点,对学生进行数学史知识的渗透,告诉学生导数的由来、发展和在实际生活、工作中的作用。这样就可以调动学生积极性,撇去导数的枯燥乏味,使之变为活泛、有趣。②数学思想方法的渗透a.极限思想。在导数部分主要体现在函数的连续性,导数的计算,以及定积分内容上。b.数形结合思想。数形结合在导数以及应用部分的主要表现是对函数图像的分析与求解。函数对象是导数的主要研究对象之一。要求证函数的解析式就必须进行数形结合。③数学思维方式的渗透在“导数”部分主要的数学思维方式有两种:观察法和归纳法。比如观察法在人教版A版中,导数及其应用部分主要培养了学生的观察能力。教材利用三个不同维度的观察使得学生在导数的概念、导数的运算、导数的应用之间关系的思考。归纳法是从特殊到一般再到特殊的过程,在人教版教材中主要体现在当∆x趋于0的计算。
(2)①有利于激发学生的学习兴趣数学文化给学生带来的不仅仅是数学命题、数学方法、数学问题和数学语言等,还包括数学思想、数学意识、数学精神等。在教学中可以适当的对学生进行数学文化的教育,如通过数学家的故事,数学问题的发现等内容的介绍来激发学生的学习兴趣。②有利于培养学生的创新意识和探索精神新一轮数学改革的理念中,强调培养学生的创新意识和探索精神。培养学生的数学思维能力,也是当代数学教育改革的核心问题之一。在数学文化中数学历史事件、历史过程、历史故事都能够激发起学生的创新意识,培养学生的探索精神。③有利于发展学生的数学应用意识数学文化的意义不仅在于知识本身和它的内涵,还在于它的应用价值数学源于生活,其理论的核心部分都是在人类社会的生产、生活实践之中发展起来的。因此,教学中我们应当有意识地结合学生已有的知识结构,加强数学与实际生活的联系。增强数学的应用性,将数学知识生活化,让学生体验到数学文化的价值就在于生活的各个领域中都要用到数学。
真题5:《课程标准》在数学建议中指出应当处理好“面向全体学生与关注学生个体差异的关系”,论述数学教学中如何理解和处理这一关系。
教学活动应努力使全体学生达到课程目标的基本要求,同时要关注学生的个体差异,促进每个学生在原有基础上的发展.①对于学习有困难的学生,教师要A.给予及时的关注与帮助;B.鼓励他们主动参与数学学习活动,并尝试用自己的方式解决问题、发表自己的看法;C.要及时地肯定他们的点滴进步;D.耐心地引导他们分析产生困难或错误的原因,并鼓励他们自己去改正,从而增强学习数学的兴趣和信心。②对于学有余力并对数学有兴趣的学生,教师要为他们提供足够的材料和思维空间,指导他们阅读,发展他们的数学才能。③在教学活动中,要鼓励与提倡解决问题策略的多样化,恰当评价学生在解决问题过程中所表现出的不同水平。④问题情境的设计、教学过程的展开、练习的安排等要尽可能地让所有学生都能主动参与,提出各自解决问题的策略。⑤引导学生通过与他人的交流选择合适的策略,丰富数学活动的经验,提高思维水平。
最后,华图教师预祝广大考生考试顺利,乘华图翅膀,圆教师梦想!

 女痞
女痞
 人生岁月几度寒
人生岁月几度寒