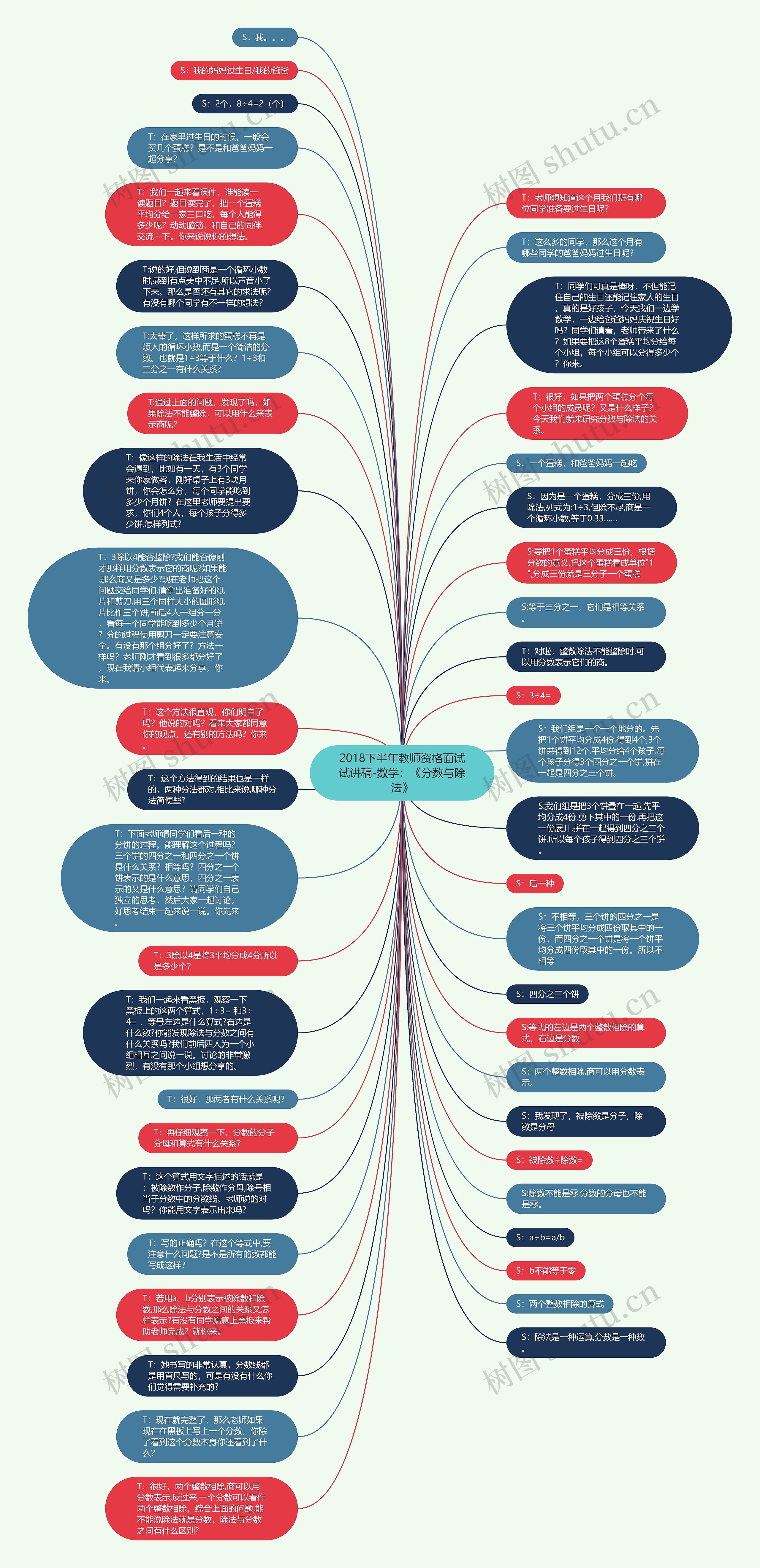
T:老师想知道这个月我们班有哪位同学准备要过生日呢?
T:这么多的同学,那么这个月有哪些同学的爸爸妈妈过生日呢?
T:同学们可真是棒呀,不但能记住自己的生日还能记住家人的生日,真的是好孩子,今天我们一边学数学,一边给爸爸妈妈庆祝生日好吗?同学们请看,老师带来了什么?如果要把这8个蛋糕平均分给每个小组,每个小组可以分得多少个?你来。
T:很好,如果把两个蛋糕分个每个小组的成员呢?又是什么样子?今天我们就来研究分数与除法的关系。
T:在家里过生日的时候,一般会买几个蛋糕?是不是和爸爸妈妈一起分享?
T:我们一起来看课件,谁能读一读题目?题目读完了,把一个蛋糕平均分给一家三口吃,每个人能得多少呢?动动脑筋,和自己的同伴交流一下。你来说说你的想法。
S:因为是一个蛋糕,分成三份,用除法,列式为:1÷3,但除不尽,商是一个循环小数,等于0.33……
T:说的好,但说到商是一个循环小数时,感到有点美中不足,所以声音小了下来。那么是否还有其它的求法呢?有没有哪个同学有不一样的想法?
S:要把1个蛋糕平均分成三份,根据分数的意义,把这个蛋糕看成单位"1",分成三份就是三分子一个蛋糕
T:太棒了。这样所求的蛋糕不再是烦人的循环小数,而是一个简洁的分数。也就是1÷3等于什么?1÷3和三分之一有什么关系?
T:通过上面的问题,发现了吗,如果除法不能整除,可以用什么来表示商呢?
T:对啦,整数除法不能整除时,可以用分数表示它们的商。
T:像这样的除法在我生活中经常会遇到,比如有一天,有3个同学来你家做客,刚好桌子上有3块月饼,你会怎么分,每个同学能吃到多少个月饼?在这里老师要提出要求,你们4个人,每个孩子分得多少饼,怎样列式?
T:3除以4能否整除?我们能否像刚才那样用分数表示它的商呢?如果能,那么商又是多少?现在老师把这个问题交给同学们,请拿出准备好的纸片和剪刀,用三个同样大小的圆形纸片比作三个饼,前后4人一组分一分,看每一个同学能吃到多少个月饼?分的过程使用剪刀一定要注意安全。有没有那个组分好了?方法一样吗?老师刚才看到很多都分好了,现在我请小组代表起来分享。你来。
S:我们组是一个一个地分的。先把1个饼平均分成4份,得到4个,3个饼共得到12个,平均分给4个孩子,每个孩子分得3个四分之一个饼,拼在一起是四分之三个饼。
T:这个方法很直观,你们明白了吗?他说的对吗?看来大家都同意你的观点,还有别的方法吗?你来。
S:我们组是把3个饼叠在一起,先平均分成4份,剪下其中的一份,再把这一份展开,拼在一起得到四分之三个饼,所以每个孩子得到四分之三个饼。
T:这个方法得到的结果也是一样的,两种分法都对,相比来说,哪种分法简便些?
T:下面老师请同学们看后一种的分饼的过程。能理解这个过程吗?三个饼的四分之一和四分之一个饼是什么关系?相等吗?四分之一个饼表示的是什么意思,四分之一表示的又是什么意思?请同学们自己独立的思考,然后大家一起讨论。好思考结束一起来说一说。你先来。
S:不相等,三个饼的四分之一是将三个饼平均分成四份取其中的一份,而四分之一个饼是将一个饼平均分成四份取其中的一份。所以不相等
T:我们一起来看黑板,观察一下黑板上的这两个算式,1÷3= 和3÷4= ,等号左边是什么算式?右边是什么数?你能发现除法与分数之间有什么关系吗?我们前后四人为一个小组相互之间说一说。讨论的非常激烈,有没有那个小组想分享的。
T:再仔细观察一下,分数的分子分母和算式有什么关系?
T:这个算式用文字描述的话就是:被除数作分子,除数作分母,除号相当于分数中的分数线。老师说的对吗?你能用文字表示出来吗?
T:写的正确吗?在这个等式中,要注意什么问题?是不是所有的数都能写成这样?
T:若用a、b分别表示被除数和除数,那么除法与分数之间的关系又怎样表示?有没有同学愿意上黑板来帮助老师完成?就你来。
T:她书写的非常认真,分数线都是用直尺写的,可是有没有什么你们觉得需要补充的?
T:现在就完整了,那么老师如果现在在黑板上写上一个分数,你除了看到这个分数本身你还看到了什么?
T:很好,两个整数相除,商可以用分数表示,反过来,一个分数可以看作两个整数相除,综合上面的问题,能不能说除法就是分数,除法与分数之间有什么区别?
 U633687664
U633687664
 U582679646
U582679646