2021年教师资格证考试历年真题：初中数学试讲思维导图

宠上天

2023-03-13

浏览量: 2

教师资格证考试

2021教师资格证

教师资格证笔试

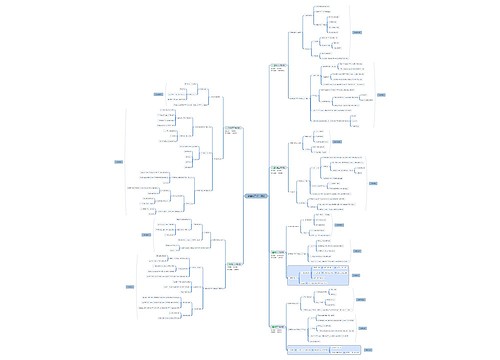
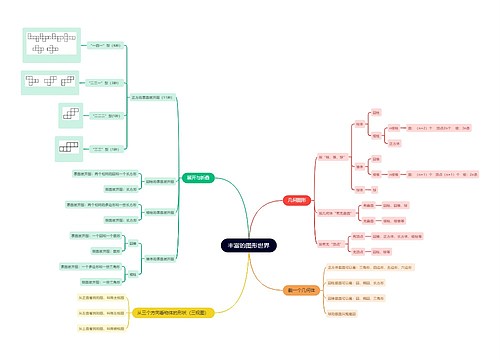
2021年教师资格证考试历年真题：初中数学试讲思维导图，本模板着重介绍了勾股定理的逆定理，逆定理与原定理的题设和结论正好相反，本模板通过导图的形式向学生展示了如何证明勾股定理的逆定理，并进行了解释和概括，本模板还说明了不同命题之间的逆命题成立情况可能不同，需要多加辨析。试讲过程中，教师通过复习旧知、导入新课方式引导学生，重点突出，条理清晰，让学生在短时间内理解并掌握了勾股定理的逆定理。

思维导图大纲

内容：

命题2 如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形。

我们看到，命题2与上节的命题1的题设、结论正好相反。我们把像这样的两个命题叫做互逆命题。如果把其中一个叫做原命题，那么另一个叫做它的逆命题。例如，如果把命题1当成原命题，那么命题2是命题1的逆命题。上节已证明命题1正确，能证明命题2正确吗？

在图17.2-2（1）中，已知△ABC的三边长分别为a，b，c，且满足a²+b²=c²，要证△ABC一定是直角三角形。我们可以先画一个两条直角边长分别为a，b的直角三角形，如果△ABC与这个直角三角形全等，那么△ABC就是一个直角三角形。

如图17.2-2（2），画一个Rt△A'B'C'，使B'C'=a，A'C'=b，∠C'=90°。根据勾股定理，A'B'²=B'C'²+A'C'²=a²+b²=c²，得A'B'=c。在△ABC和△A'B'C'中，BC=a=B'C'，AC=b=A'C'，AB=c=A'B'，所以△ABC≌△A'B'C'。因此∠C=∠C'=90°，即△ABC是直角三角形。

这样我们证明了勾股定理的逆命题是正确的，它也是一个定理。我们把这个定理叫做勾股定理的逆定理。它是判定直角三角形的一个依据。

一般地，原命题成立时，它的逆命题可能成立，也可能不成立。如本章中的命题1成立，它的逆命题命题2也成立；命题“对顶角相等”成立，而它的逆命题“如果两个角相等，那么这两个角是对顶角”却不成立。

基本要求：

（1）有合适的板书；

（2）引导学生猜想、证明勾股定理的逆定理；

（3）教学中注意条理清晰，重点突出；

（4）请在10分钟内完成试讲内容。

答辩题目：

1.谈一谈勾股定理在初中教材中的地位。

2.教学过程中你主要设置了哪些问题？目的是什么？

试讲答案：

各位考官：大家好，我是初中数学组的XX号考生，今天我试讲的题目是《勾股定理的逆定理》，下面开始我的试讲。

一、复习旧知，导入新课

师：上一节课我们学习了勾股定理，请同学们回忆一下勾股定理的内容是什么？

师：对，勾股定理反映了直角三角形三边之间的数量关系，若直角三角形的两直角边长为a，b，斜边长为c，则三边长满足a²+b²=c²。请同学们思考一下，勾股定理的题设、结论分别是什么？

师：大家说得很好，题设是直角三角形的两条直角边长为a，b，斜边为c，结论为三边长满足a²+b²=c²。如果把勾股定理的题设、结论交换一下位置，命题还成立吗？即如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形吗？本节课我们就一起来学习《勾股定理的逆定理》。

二、结合实例，讲解新知

师：据说古埃及人画直角的方法是把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角。用这样的绳结组成的三角形是直角三角形吗？请同学们画画看，并用量角器检验一下。

师：大家测量出来有一个角是直角，也就是说，如果围成的三角形的三边长分别为3，4，5，那么围成的三角形是直角三角形，这里的3，4，5有什么关系呢？

师：有同学发现了，3²+4²=5²。那再画画看，如果三角形的三边长分别为2.5²cm、6²cm、6.5²cm，并有2.5²+6²=6.5²，画出的三角形是直角三角形吗？换成三边长分别为6cm、8cm、10cm呢？同学们在小组内动手画一画并测量一下是否构成直角。

师：大家根据以上的发现能得出什么猜想？

师：很好，同学们发现如果围成的三角形的三边长满足a²+b²=c²的关系，那么这三边围成的三角形恰好是直角三角形。我们进而会想：是不是三角形的三边只要有两边的平方和等于第三边的平方，就能得到一个直角三角形呢？我们得出一个猜想的命题：

命题2：如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形。

师：猜想的命题2正确吗？你能证明它吗？也就是说，已知△ABC三边长a，b，c满足a²+b²=c²，求证△ABC是直角三角形。

师：要证明△ABC是直角三角形，我们需要知道∠C是直角，那么如何证明∠C是直角呢？

师：我们一起来试试再作一个Rt△A'B'C'，使∠C'=90°，且A'C'=AC，B'C'=BC，则满足A'C'²+B'C'²=A'B'²（勾股定理），你们能利用全等三角形的知识验证我们要证明的命题吗？大家在小组内探讨一下。

师：第1小组已经探讨出来了，你们先说一下你们的证明思路吧！

师：第1小组是这样证明的：∵AC²+BC²=AB²（已知），A'C'=AC，B'C'=BC（已作），∴AB²=A'B'²，∴AB=A'B'∴△ABC≌△A'B'C'，∴∠C=∠C'=90°，∴△ABC是直角三角形。

师：通过刚才的证明，我们可以得出前面的猜想是正确的，我们把它称为勾股定理的逆定理。即要判断一个三角形是否为直角三角形，只需要知道三边能否满足“两边的平方和等于第三边的平方”，即“较小的两边的平方和等于较长边的平方”，如果满足，则为直角三角形。

师：我们得出的命题2与之前学过的命题1有什么联系呢？

师：学生1说这两个命题的题设和结论正好相反。在数学上，像这样的两个命题我们叫做互逆命题。你们能举出互逆命题的例子吗？

师：很好，大家想一想你所举的例子中，如果原命题成立，逆命题一定成立吗？

师：我们不难发现原命题与逆命题是否成立是相互独立的。

三、练习巩固

师：我们来看一看例题：判断由线段a，b，c组成的三角形是不是直角三角形。（1）a=15，b=8，c=17；（2）a=13，b=14，c=15。

师：勾股定理的逆定理在已知三角形的三边长时，可以用来判断该三角形是否为直角三角形。下面请同学们以小组为单位合作交流，完成例题。

师：哪位同学来展示一下你们组的答案？

师：很好，那我们一起来验证学生2所在小组的答案。题目（1）中15²+8²=225+64=289=17²，所以这个三角形是直角三角形。题目（2）中13²+14²=169+196=365≠15²，所以这个三角形不是直角三角形。

四、课堂小结

师：谁能来总结一下，已知三角形的三边长，如何判断这个三角形是否为直角三角形？

师：总结得很好，只需要看三角形的三边是否满足“两边的平方和等于第三边的平方”，如果是，则是直角三角形，反之不是。

五、板书设计

勾股定理的逆定理

命题2：如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形是直角三角形。（勾股定理的逆定理）

互逆命题原命题逆命题

例题：判断由线段a，b，c组成的三角形是不是直角三角形。

（1）a=15，b=8，c=17；

（2）a=13，b=14，c=15。

解：（1）15²+8²=225+64=289=17²，∴这个三角形是直角三角形。

（2）13²+14²=169+196=365≠15²，∴这个三角形不是直角三角形。

我的试讲到此结束，谢谢各位考官的聆听。

答辩答案：

1.勾股定理是初中几何中几个重要定理之一。它揭示了直角三角形三边的某种数量关系。勾股定理是建立在三角形、全等三角形、等腰三角形等有关知识的基础之上的，同时也是初三几何中解直角三角形及圆中有关计算的必备知识。更重要的是，纵观整个初中数学，勾股定理架起了代数与几何之间的桥梁。勾股定理在数学理论体系中的地位举足轻重，就学生而言，对勾股定理学习的好坏将直接影响到他们后续数学的学习。

2.第一个问题：引入古埃及人画直角的方法：把一根长绳打上13个绳结，以3，4，5个结间距为边长组成的三角形中就有一个角是直角。让学生测量用这样的绳结组成的三角形是否是直角三角形。

设计意图：通过古代数学问题激发学生的学习兴趣，从而为得出勾股定理的逆定理做铺垫。

第二个问题：让学生动手操作，导入问题，让学生判断三边长分别为2.5cm，6cm，6.5cm或4cm、7.5cm、8.5cm时是否满足a²+b²=c²，能否组成直角三角形，根据以上结论得出猜想。

设计意图：鼓励学生动手探究，提升综合实践能力，进一步根据事实作出猜想，提升合情推理能力。

第三个问题：让学生证明所猜想的命题是否正确。

设计意图：鼓励学生对猜想进行证明，养成良好的反思质疑的学习习惯，进一步提升演绎推理能力。

第四个问题：让学生来总结，已知三角形的三边长，如何判断这个三角形是否为直角三角形。

设计意图：课堂最后通过总结回顾，帮助学生梳理要点，回顾解答过程，让理解更深刻，学习更有效。

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图