树图网

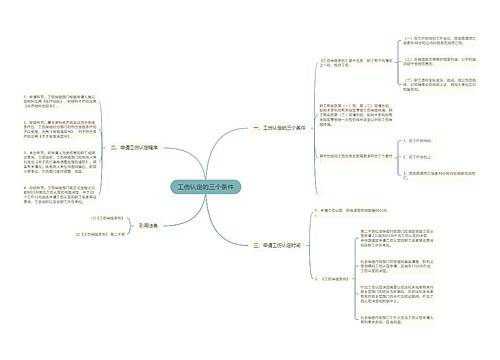
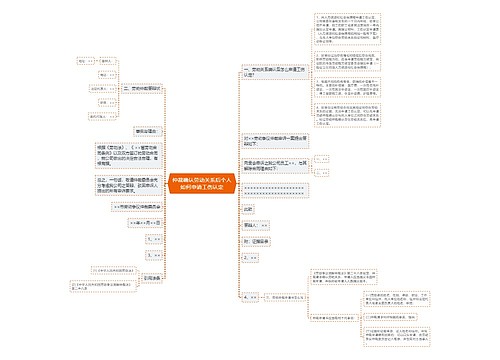
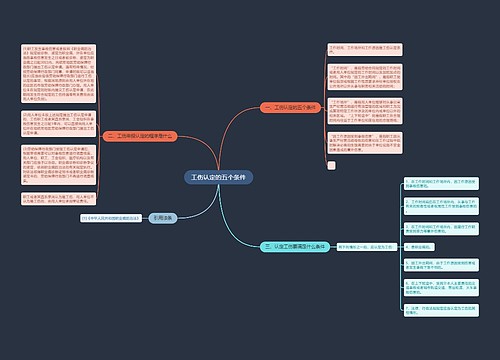
行测知识点：轴对称图形细化考点梳理思维导图

孤败
2023-03-04
浏览量: 4
行测知识点：轴对称图形细化考点梳理
行测备考
知识点

对称性一直作为图形推理当中的高频考点，不断地被考察，近几年的考察也随着考点的深入和变化，更多的与其他考点融合。

树图思维导图提供《行测知识点：轴对称图形细化考点梳理》在线思维导图免费制作，点击“编辑”按钮，可对《行测知识点：轴对称图形细化考点梳理》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：8ce267ee07ba260c0ad6ce056a0e4699

思维导图大纲

相关思维导图模版

《深入推进“知鑫服务直通车”行动计划（2024—2026年）》思维导图
U170141402
2.34
树图思维导图提供《《深入推进“知鑫服务直通车”行动计划（2024—2026年）》》在线思维导图免费制作，点击“编辑”按钮，可对《《深入推进“知鑫服务直通车”行动计划（2024—2026年）》》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：48c6d575faeddbf64435f55537f6c6a6
《深入推进“知鑫服务直通车”行动计划（2024—2026年）》
销售订单下单交付过程优化梳理思维导图
U369999453
4.55
树图思维导图提供《销售订单下单交付过程优化梳理》在线思维导图免费制作，点击“编辑”按钮，可对《销售订单下单交付过程优化梳理》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：ed20dbe621fa2100ae711f4a1a3b9bc5
销售订单下单交付过程优化梳理
思维导图模板资格考试公务员考试正文

相似思维导图模版

行测知识点（三）思维导图
2022-08-15 19:34:02
行测知识点（三）
到二〇二五年新型储能步入规模化发展阶段思维导图
2023-03-08 10:54:32
到二〇二五年新型储能步入规模化发展阶段
身心发展思维导图
2022-04-03 19:48:41
身心发展
公基财政学导论思维导图
2022-08-10 20:54:34
公基财政学导论思维导图
行测各模块复习重点思维导图
2022-08-09 10:19:28
行测各模块复习重点思维导图
公基法理学思维导图
2022-07-27 22:20:17
公基法理学思维导图

思维导图模版推荐

工伤认定的三个条件思维导图
2023-03-04 05:37:03
工伤认定的三个条件
2022年国考判断推理备考干货之外延关系思维导图
2023-03-04 05:37:06
2022年国考判断推理备考干货之外延关系
仲裁确认劳动关系后个人如何申请工伤认定思维导图
2023-03-04 05:37:08
仲裁确认劳动关系后个人如何申请工伤认定
工伤认定去哪个部门思维导图
2023-03-04 05:36:59
工伤认定去哪个部门
工伤认定的五个条件思维导图
2023-03-04 05:36:55
工伤认定的五个条件
2022国考行测备考干货内涵关系之对应关系思维导图
2023-03-04 05:36:51
2022国考行测备考干货内涵关系之对应关系
首页
我的文件
我的团队
个人中心