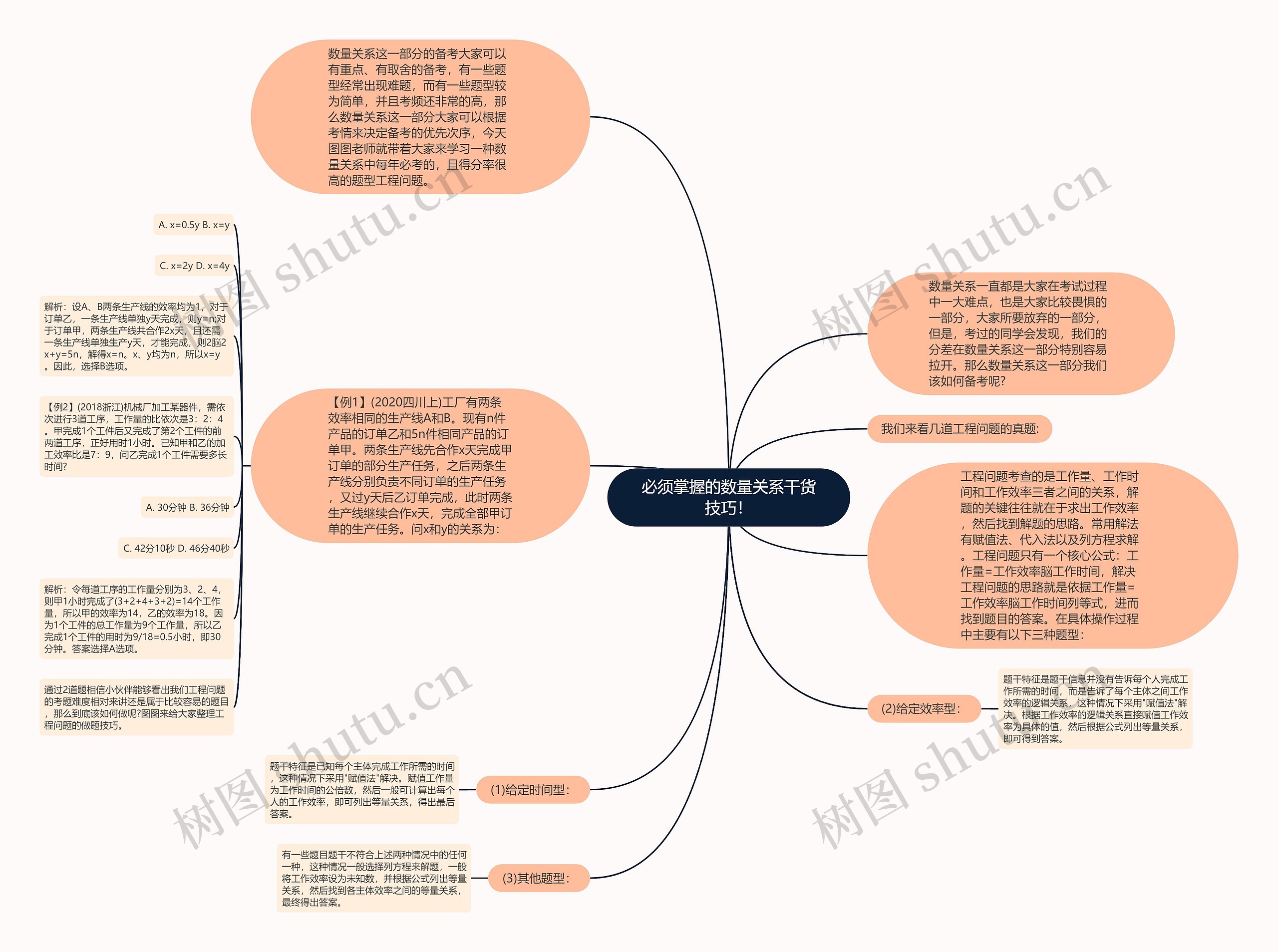
数量关系一直都是大家在考试过程中一大难点,也是大家比较畏惧的一部分,大家所要放弃的一部分,但是,考过的同学会发现,我们的分差在数量关系这一部分特别容易拉开。那么数量关系这一部分我们该如何备考呢?
数量关系这一部分的备考大家可以有重点、有取舍的备考,有一些题型经常出现难题,而有一些题型较为简单,并且考频还非常的高,那么数量关系这一部分大家可以根据考情来决定备考的优先次序,今天图图老师就带着大家来学习一种数量关系中每年必考的,且得分率很高的题型工程问题。
【例1】(2020四川上)工厂有两条效率相同的生产线A和B。现有n件产品的订单乙和5n件相同产品的订单甲。两条生产线先合作x天完成甲订单的部分生产任务,之后两条生产线分别负责不同订单的生产任务,又过y天后乙订单完成,此时两条生产线继续合作x天,完成全部甲订单的生产任务。问x和y的关系为:
解析:设A、B两条生产线的效率均为1,对于订单乙,一条生产线单独y天完成,则y=n;对于订单甲,两条生产线共合作2x天,且还需一条生产线单独生产y天,才能完成,则2脳2x+y=5n,解得x=n。x、y均为n,所以x=y。因此,选择B选项。
【例2】(2018浙江)机械厂加工某器件,需依次进行3道工序,工作量的比依次是3:2:4。甲完成1个工件后又完成了第2个工件的前两道工序,正好用时1小时。已知甲和乙的加工效率比是7:9,问乙完成1个工件需要多长时间?
解析:令每道工序的工作量分别为3、2、4,则甲1小时完成了(3+2+4+3+2)=14个工作量,所以甲的效率为14,乙的效率为18。因为1个工件的总工作量为9个工作量,所以乙完成1个工件的用时为9/18=0.5小时,即30分钟。答案选择A选项。
通过2道题相信小伙伴能够看出我们工程问题的考题难度相对来讲还是属于比较容易的题目,那么到底该如何做呢?图图来给大家整理工程问题的做题技巧。
工程问题考查的是工作量、工作时间和工作效率三者之间的关系,解题的关键往往就在于求出工作效率,然后找到解题的思路。常用解法有赋值法、代入法以及列方程求解。工程问题只有一个核心公式:工作量=工作效率脳工作时间,解决工程问题的思路就是依据工作量=工作效率脳工作时间列等式,进而找到题目的答案。在具体操作过程中主要有以下三种题型:
(1)给定时间型:
题干特征是已知每个主体完成工作所需的时间,这种情况下采用"赋值法"解决。赋值工作量为工作时间的公倍数,然后一般可计算出每个人的工作效率,即可列出等量关系,得出最后答案。
(2)给定效率型:
题干特征是题干信息并没有告诉每个人完成工作所需的时间,而是告诉了每个主体之间工作效率的逻辑关系,这种情况下采用"赋值法"解决。根据工作效率的逻辑关系直接赋值工作效率为具体的值,然后根据公式列出等量关系,即可得到答案。
(3)其他题型:
有一些题目题干不符合上述两种情况中的任何一种,这种情况一般选择列方程来解题,一般将工作效率设为未知数,并根据公式列出等量关系,然后找到各主体效率之间的等量关系,最终得出答案。
 U633687664
U633687664
 U582679646
U582679646