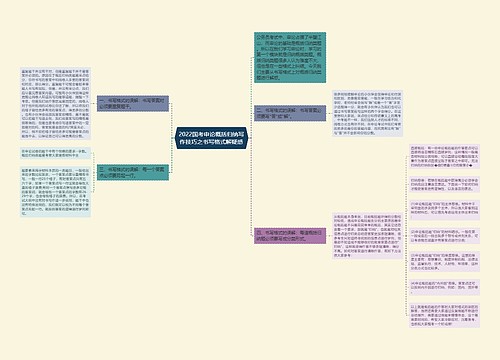
2022国笔行测备考干货 集合推理谬误浅析思维导图
旧人不归
2023-03-04

集合推理这两年在陕西的笔试考试中,呈现的占比趋势像极了波浪线,经历了由必考题目到零考察又到部分考察的特征,而作为形式推理体系当中比较重要的一类试题,也往往是考生在操作层面上最容易做错的题目之一。
树图思维导图提供《2022国笔行测备考干货 集合推理谬误浅析》在线思维导图免费制作,点击“编辑”按钮,可对《2022国笔行测备考干货 集合推理谬误浅析》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:98404425f77e65eab96edf5ac5dd8f10
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
 U633687664
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作,点击“编辑”按钮,可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:10b9a8a2dd2fb4593f8130ef16c320fc

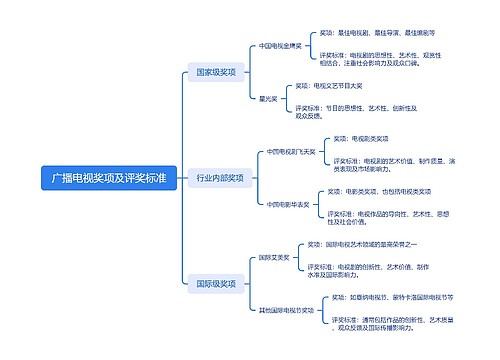
广播电视奖项及评奖标准思维导图
 U782682106
U782682106树图思维导图提供《广播电视奖项及评奖标准》在线思维导图免费制作,点击“编辑”按钮,可对《广播电视奖项及评奖标准》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:a4210651fa3a78355ac9f5101bb2c616