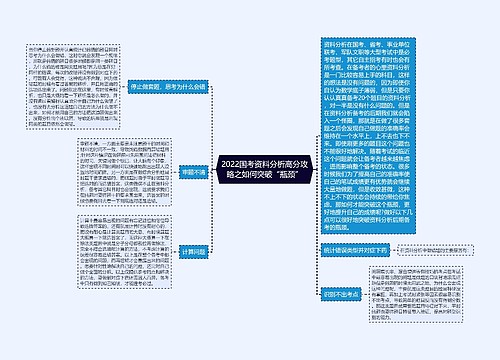
2022国考行测数资干货之环形相遇及追及思维导图
女痞
2023-03-04
数量关系科目内的行程问题可以说是公务员考试中都必考的一类题型，这是令广大考生又爱又恨的一类题目，一方面因为这类题目比较具体直观，与大家的平时生活比较贴近，题目理解起来没有太大的难度。
树图思维导图提供《2022国考行测数资干货之环形相遇及追及》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测数资干货之环形相遇及追及》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：d631accf593e373e5ced530746fa6966
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
广播电视奖项及评奖标准思维导图
U782682106树图思维导图提供《广播电视奖项及评奖标准》在线思维导图免费制作，点击“编辑”按钮，可对《广播电视奖项及评奖标准》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：a4210651fa3a78355ac9f5101bb2c616
