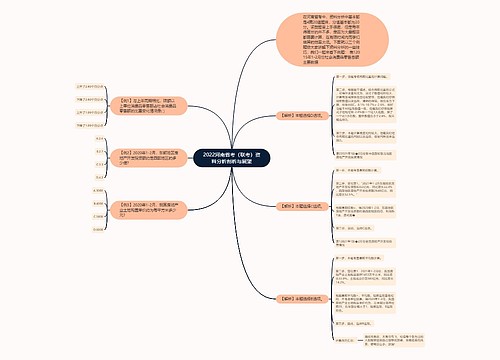
国考行测之走进“数“看清约数和倍数思维导图

深知他心

2023-03-04

浏览量: 7

国考

行测

约数

倍数

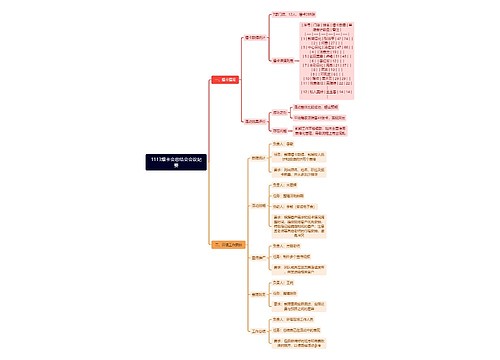
走进”数“的世界之约数与倍数，此类内容在公务员考试当中频率相对适中，主要涉及的考点有倍数特性，植树问题找最大公约数或者最小公倍数也会考察因式分解等。

树图思维导图提供《国考行测之走进“数“看清约数和倍数》在线思维导图免费制作，点击“编辑”按钮，可对《国考行测之走进“数“看清约数和倍数》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：7ab14e13f380cd23b3c839fb4e33c5e9

思维导图大纲

当题目满足：M=A脳B形式，即M是A和B的倍数，A和B是M的约数。

【引例1】某电器工作功耗为370瓦，待机状态下功耗为37瓦，该电器周一从9：30到17：00处于工作状态，其余时间断电。周二从9：00到24：00处于待机状态，其余时间断电，问其周一的耗电量是周二的多少倍?( )

A.10

B.6

C.8

D.5

【答案】D

【解析】第一步，本题考查约数和倍数问题。

第二步，根据公式耗电量(倍数)=功耗(约数)脳时间(约数)，由题意可知周一工作状态时间为7.5小时，对应工作功耗为370瓦，即周一耗电量=370脳7.5;周二待机时间为15小时，对应待机功耗为37瓦，即周二耗电量=37脳15则周一是周二的=5倍。

因此，本题选择D选项。

【引例2】对100个编号为1~100的罐子，第1个人在所有的编号为1的

倍数的罐子中倒入1毫升水，第2个人在所有编号为2的倍数的罐子中倒入1毫升水鈥︹�ψ詈蟮�100个人在所有编号为100的倍数的罐子中倒入1毫升水，问此时第92号罐子中装了多少毫升的水?( )

A.2

B.6

C.46

D.92

【答案】B

【解析】第一步，本题考查约数倍数问题。

第二步，92因式分解为：92=1脳92=2脳46=4脳23，故92的约数有1、2、4、23、46、92共6个，即有6人向92号罐子中倒水，第92号罐子中装了6毫升的水。

因此，本题选择B选项。

这两道题考察简单的约数和倍数问题，只要题目满足：M=A脳B=1脳M形式，即M是A和B的倍数。A和B是M的约数。我们来再通过二道题来帮大家分析何为最大公约数，何为最小公倍数。无论最大公约数还是最小公倍数都需要大家使用短除法找到对应的数据。

【真题1】为加强治安防控，现计划在一段L形的围墙(如下图)上安装治安摄像头，其中A点到B点长度为750米，B点到C点长度为1350米。按要求ABC三个位置必须安装一个摄像头，且相邻两个摄像头之间的距离要保持一致，则整段围墙至少需要安装( )个摄像头。

A.14

B.15

C.16

D.17

【答案】B

【解析】第一步，本题考查植树问题。

第二步，要想安装的摄像头少则间距尽可能大，因为要求间距相等，则间距应为750和1350的最大公约数，750和1350因式分解为：750=150脳5和1350=150脳9，即最大公约数为150，故选择150米作为间距。道路总长750+1350=2100(米)，根据直线单侧植树公式，棵数=总长梅间距+1，可知需要安装摄像头2100梅150+1=15(个)。因此，本题选择B选项。

【真题2】三个学校的志愿队分别去敬老院照顾老人，A学校志愿队每隔7天去一次，B学校志愿队每隔9天去一次，C学校志愿队每隔14天去一次，三个队伍周三第一次同时去敬老院，问下次同时去敬老院是周几?( )

A.周三

B.周四

C.周五

D.周六

【答案】B

【解析】第一步，本题考查星期日期问题，需要结合最小公倍数知识点解题。第二步，A、B、C三个学校志愿队每隔7天，每隔9天，每隔14天，相当于三个学校去敬老院的周期分别为每8天，每10天、每15天，故下一次同时去敬老院的时间为120天=2脳4脳3脳5(8、10、15的最小公倍数)后。因为120梅7=17鈥�1，所以周三之后再过120天为周四。

因此，本题选择B选项。

注意：每隔n天=每n+1天。

总体来说此类题型并不难，只需要同学们会找最大公约数和最小公倍，那约数和倍数就可以迎刃而解。希望各位小伙伴们在今后的学习中，多去练习多刷题。在此再附上一张思维导图，方便大家记忆。

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图