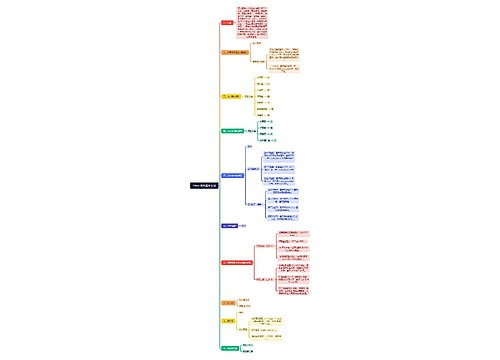
2022国考行测备考之基础概率思维导图
眼眶很热
2023-03-04
小伙伴们好，在备考之中，概率问题也是常规考点之一，但是部分小伙伴对于这一部分知识不是很熟练，甚至“谈虎色变”。其实概率与我们的生活紧密相连，密不可分。下面我们再对基础概率进行一些展开，相信小伙伴们看了后能有所启发，对概率问题形成一定改观。
树图思维导图提供《2022国考行测备考之基础概率》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测备考之基础概率》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：50bbd4acb52499a8310a69f23113f6ce
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
Linux 网络基础知识思维导图
U880113127树图思维导图提供《Linux 网络基础知识》在线思维导图免费制作，点击“编辑”按钮，可对《Linux 网络基础知识》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：199680f0e48eac8a1aeaadb90447d4f4
