国考行测：真假推理什么时候需要再推一步思维导图

叹黄昏

2023-03-04

浏览量: 2

国考行测：真假推理什么时候需要再推一步

国考

行测

真假推理

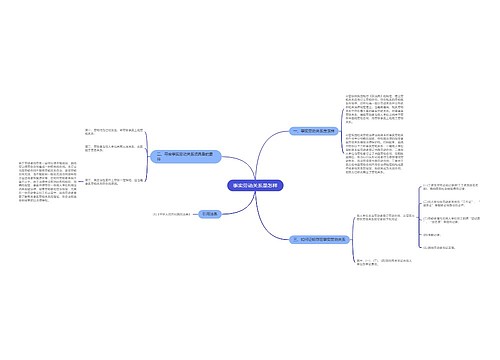
接触过真假推理这一模块的同学会发现，只要记住我们所学的六组矛盾关系和两组反对关系，做题就比较简单，只用遵循“找关系-看其余”的做题思路往往就能迎刃而解，但有的同学会发现，有一些题目中看其余没办法选择到正确答案

树图思维导图提供《国考行测：真假推理什么时候需要再推一步》在线思维导图免费制作，点击“编辑”按钮，可对《国考行测：真假推理什么时候需要再推一步》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：56c9a490d1b7e299393eaf718a84e00e

思维导图大纲

相关思维导图模版

国考行测：真假推理什么时候需要再推一步思维导图模板大纲

接触过真假推理这一模块的同学会发现，只要记住我们所学的六组矛盾关系和两组反对关系，做题就比较简单，只用遵循"找关系-看其余"的做题思路往往就能迎刃而解，但有的同学会发现，有一些题目中看其余没办法选择到正确答案，这时候就需要我们往后"推一步"，那我们就来看一看具体什么样子的题目，需要"往后推一步"以及需要"怎么推"。

【例1】实验室有四个烧杯，每个烧杯下放置一张小纸条：第一个写着"所有的烧杯中都有硫酸";第二个写着"本杯是氯化钠";第三个写着"本杯不是水";第四个写着"有些烧杯中没有硫酸"。

如果这四个烧杯对应的话只有一句是真的，那么以下哪项必定为真?

A.第一个烧杯中是硫酸

B.第二个烧杯中是氯化钠

C.第三个烧杯中是水

D.第四个烧杯中不是硫酸

【答案】C

【解析】

第一步，确定题型。

题干有若干论断和真假设定，确定为真假推理。

第二步，找关系。

第一个写着"所有的烧杯中都有硫酸"和第四个写着"有些烧杯中没有硫酸"互为矛盾关系

第三步，看其余。

根据矛盾关系特性"必有一真，必有一假"，且"只有一句是真的"，可知第二个烧杯和第三个烧杯上写的话为假，故第二个不是氯化钠，第三个是水。

因此，选择C选项。

本题只需要判定"所有S都是P"与"有的S不是P"这一组关系为矛盾关系，存在一真一假，然后"看其余"就能选出正确答案，并无难度。

【例2】四位球迷在某球赛的晋级赛开始之前对几个队伍的赛况进行预测，他们比较关注其中的两支球队，分别作了如下预测：

方某说：如果甲队不能晋级，那么乙队也不能晋级。

白某说：不管甲队能不能晋级，乙队都不能晋级。

夏某说：乙队能晋级，但甲队不能晋级。

邓某说：我看这几支球队都不能晋级。

比赛结果证明，四位球迷中只有一位的预测是正确的。

根据上述情况，以下哪项一定为真?

A.白某预测是正确的

B.邓某预测是正确的

C.如果甲队能够晋级，那么方某的预测是正确的

D.如果甲队不能晋级，那么方某的预测是正确的

【答案】C

【解析】

第一步，确定题型。

题干有若干论断及真假限定，确定为真假推理。

第二步，找关系。

①卢甲鈫捖�

②卢乙;

③乙且卢甲;

④所有球队都不能晋级。

其中①和③是矛盾关系。

第三步，看其余。

根据矛盾关系的特性"必有一真，必有一假"及题干的真假限定"只有一位的预测是正确的"，则真话一定在①和③中，那么其余信息为假，即②白某的话和④邓某的话为假，排除A项、B项。由②为假，可以推出：乙队晋级。C项中，"甲队能够晋级"，根据"且关系"的特性"一假则假"，那么③为假，①就为真，即"方某的预测是正确的"，可以推出;D项中，"如果甲队不能晋级"，结合"乙队晋级了"，根据"且关系"的特性"全真则真"，证明③为真话，那么①为假，即方某的预测是错误的，排除。

因此，选择C选项。

看到这一题，当我们用"找关系-看其余"的解题思路来做的时候，只能排除A、B选项，剩下的B、C我们不能选择其中某一个，这时候我们就需要根据选项增添的信息再推一步，来确定这一组矛盾关系中谁真谁假，最后才能选择正确选项。

【例 3】下面是某冬日我国北方某些城市的天气情况：

(1)有些城市有降雪;

(2)有些城市没有降雪;

(3)北京和邯郸没有降雪。

如果三个断定中只有一个为真，那么以下选项中哪个断定一定为真?

A.北京有降雪，但邯郸没有

B.所有这些城市都有降雪

C.所有这些城市都没有降雪

D.以上各选项都不一定为真

第一步，确定题型。

根据若干论断和真假限定，确定为真假推理。

第二步，找关系。

(1)"有些城市有降雪"和(2)"有些城市没有降雪"为反对关系。

第三步，看其余。

根据反对关系中"两个有的，必有一真"的特性及题干的真假限定可知，真话一定在(1)和(2)中，则其余信息(3)一定为假;

根据(3)为假，可以得到"北京下雪或者邯郸下雪"为真，进而可以推出：有的地方下雪了，则可以得到(1)为真，那么(2)为假;

再根据(2)"有些城市没有降雪"为假，可以推出(2)的矛盾命题"所有的城市都降雪"为真。

因此，选择B选项。

该题也是一样的道理，只用"找关系-看其余"这一思路，只能排除错误选项A，这就需要回到题干继续寻找"有的S是P"与"有的S不是P"这对反对关系谁真谁假来选择正确选项。

综上，大家会发现，什么时候不用往后推一步：当用其余能直接选出唯一答案时，则可以直接结束本题;那什么时候需要再往后推一步呢?当用其余不能选出正确答案或有多个答案都可选择时，我们需要往后来明确这组矛盾或反对关系的真假问题，再来选择正确选项。

查看更多

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图

树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc

904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查

埃隆·马斯克的商业版图思维导图

树图思维导图提供《埃隆·马斯克的商业版图》在线思维导图免费制作，点击“编辑”按钮，可对《埃隆·马斯克的商业版图》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：7464362ac911e8a334867bb3fc7a2346

埃隆·马斯克的商业版图

思维导图模板

公务员考试

正文

相似思维导图模版

行测知识点（三）思维导图

2022-08-15 19:34:02

行测知识点（三）

行测知识点（十四）思维导图

2022-08-16 10:17:45

行测知识点（十四）

行测常识：中国近代史时间轴思维导图

2022-07-26 20:47:24

行测常识：中国近代史时间轴

公考基30个必知汇总树形图思维导图

2022-07-20 18:45:19

公考基30个必知汇总树形图

国考行测——资料分析考点思维导图

2022-07-03 17:46:50

国考行测——资料分析考点

公考政治常识马哲思维导图

2022-07-27 13:03:33

公考政治常识马哲思维导图

思维导图模版推荐

事实劳动关系是怎样思维导图

2023-03-04 00:45:24

事实劳动关系是怎样

军队文职面试的这些事你了解吗?思维导图

2023-03-04 00:45:25

军队文职面试的这些事你了解吗?

2022行测干货之类比推理——聊聊“二级辨析”那些事儿思维导图

2023-03-04 00:45:30

2022行测干货之类比推理——聊聊“二级辨析”那些事儿

劳动关系是什么思维导图

2023-03-04 00:45:19

劳动关系是什么

2022国考行测备考之分析推理“一拖五”如何提高？思维导图

2023-03-04 00:45:17

2022国考行测备考之分析推理“一拖五”如何提高？

劳动关系是什么意思思维导图

2023-03-04 00:45:15

劳动关系是什么意思

首页

我的文件

我的团队

个人中心