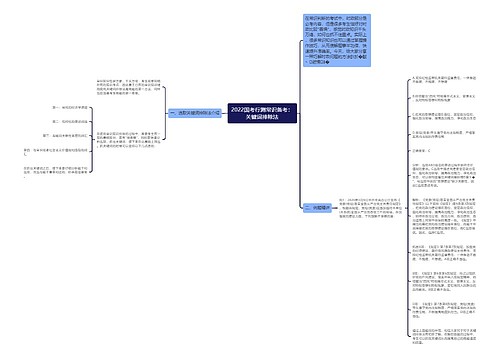
2022国考行测行程问题：多次相遇追及思维导图
催眠
2023-03-03
行程问题在大多数同学的脑海里就是一团乱麻，剪不断，理还乱，尤其是多次相遇追及问题，相遇个两次三次还能勉强理清楚，但是相遇次数过多，那就基本是OVER!其实大多数多次相遇追及问题并不是那么可拍，而是“纸老虎”，只需要一个公式就能一步到位得出答
树图思维导图提供《2022国考行测行程问题：多次相遇追及》在线思维导图免费制作，点击“编辑”按钮，可对《2022国考行测行程问题：多次相遇追及》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：0ce1970960d607e4127c1546f320eab2
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
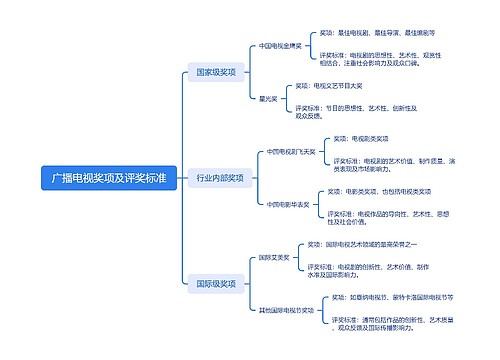
广播电视奖项及评奖标准思维导图
U782682106树图思维导图提供《广播电视奖项及评奖标准》在线思维导图免费制作，点击“编辑”按钮，可对《广播电视奖项及评奖标准》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：a4210651fa3a78355ac9f5101bb2c616
