分析推理之六面体中的移面大法思维导图
琴瑟如你
2023-03-03
判断推理当中的六面体问题是不少考生心中的“老大难”，对于空间想象能力较差的人来说做起来着实难度不小，不少考生绞尽脑汁，发明出了“橡皮法”、“折纸法”。虽然大部分省份对于能否用橡皮解题没有明确规定。
树图思维导图提供《分析推理之六面体中的移面大法》在线思维导图免费制作，点击“编辑”按钮，可对《分析推理之六面体中的移面大法》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：45fa14622d45afd8f3c15343452d7454
思维导图大纲
相关思维导图模版
904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查思维导图
U633687664树图思维导图提供《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》在线思维导图免费制作，点击“编辑”按钮，可对《904名中国成年人第三磨牙相关知识、态度、行为和病史的横断面调查》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：10b9a8a2dd2fb4593f8130ef16c320fc
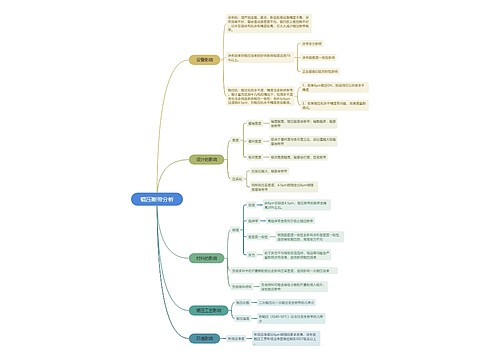
辊压断带分析思维导图
U678146910树图思维导图提供《辊压断带分析》在线思维导图免费制作，点击“编辑”按钮，可对《辊压断带分析》进行在线思维导图编辑，本思维导图属于思维导图模板主题，文件编号是：55fdf0827fa2a220b0b4047d75df5032
