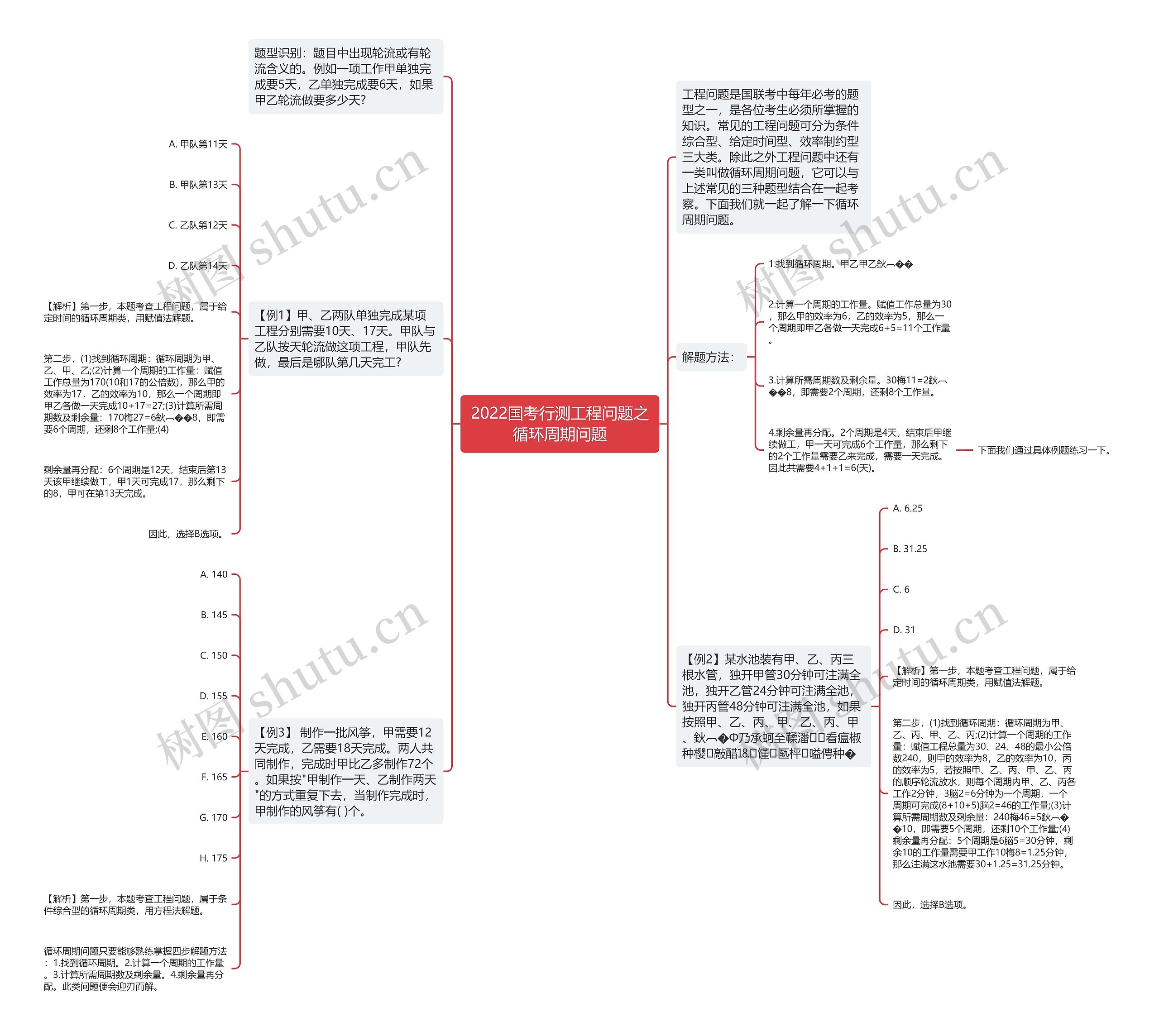
工程问题是国联考中每年必考的题型之一,是各位考生必须所掌握的知识。常见的工程问题可分为条件综合型、给定时间型、效率制约型三大类。除此之外工程问题中还有一类叫做循环周期问题,它可以与上述常见的三种题型结合在一起考察。下面我们就一起了解一下循环周期问题。
题型识别:题目中出现轮流或有轮流含义的。例如一项工作甲单独完成要5天,乙单独完成要6天,如果甲乙轮流做要多少天?
解题方法:
2.计算一个周期的工作量。赋值工作总量为30,那么甲的效率为6,乙的效率为5,那么一个周期即甲乙各做一天完成6+5=11个工作量。
3.计算所需周期数及剩余量。30梅11=2鈥︹��8,即需要2个周期,还剩8个工作量。
4.剩余量再分配。2个周期是4天,结束后甲继续做工,甲一天可完成6个工作量,那么剩下的2个工作量需要乙来完成,需要一天完成。因此共需要4+1+1=6(天)。
【例1】甲、乙两队单独完成某项工程分别需要10天、17天。甲队与乙队按天轮流做这项工程,甲队先做,最后是哪队第几天完工?
【解析】第一步,本题考查工程问题,属于给定时间的循环周期类,用赋值法解题。
第二步,(1)找到循环周期:循环周期为甲、乙、甲、乙;(2)计算一个周期的工作量:赋值工作总量为170(10和17的公倍数),那么甲的效率为17,乙的效率为10,那么一个周期即甲乙各做一天完成10+17=27;(3)计算所需周期数及剩余量:170梅27=6鈥︹��8,即需要6个周期,还剩8个工作量;(4)
剩余量再分配:6个周期是12天,结束后第13天该甲继续做工,甲1天可完成17,那么剩下的8,甲可在第13天完成。
【例2】某水池装有甲、乙、丙三根水管,独开甲管30分钟可注满全池,独开乙管24分钟可注满全池,独开丙管48分钟可注满全池,如果按照甲、乙、丙、甲、乙、丙、甲、鈥︹�Φ乃承蚵至鞣潘看瘟椒种樱敲醋⒙馑匦枰嗌俜种�
【解析】第一步,本题考查工程问题,属于给定时间的循环周期类,用赋值法解题。
第二步,(1)找到循环周期:循环周期为甲、乙、丙、甲、乙、丙;(2)计算一个周期的工作量:赋值工程总量为30、24、48的最小公倍数240,则甲的效率为8,乙的效率为10,丙的效率为5,若按照甲、乙、丙、甲、乙、丙的顺序轮流放水,则每个周期内甲、乙、丙各工作2分钟,3脳2=6分钟为一个周期,一个周期可完成(8+10+5)脳2=46的工作量;(3)计算所需周期数及剩余量:240梅46=5鈥︹��10,即需要5个周期,还剩10个工作量;(4)剩余量再分配:5个周期是6脳5=30分钟,剩余10的工作量需要甲工作10梅8=1.25分钟,那么注满这水池需要30+1.25=31.25分钟。
【例3】 制作一批风筝,甲需要12天完成,乙需要18天完成。两人共同制作,完成时甲比乙多制作72个。如果按"甲制作一天、乙制作两天"的方式重复下去,当制作完成时,甲制作的风筝有( )个。
【解析】第一步,本题考查工程问题,属于条件综合型的循环周期类,用方程法解题。
循环周期问题只要能够熟练掌握四步解题方法:1.找到循环周期。2.计算一个周期的工作量。3.计算所需周期数及剩余量。4.剩余量再分配。此类问题便会迎刃而解。
 U633687664
U633687664
 乐农
乐农